题目内容
5．
如图所示，已知OA=OB，则数轴上点A表示的数是-$\sqrt{5}$．
分析 根据勾股定理可以求得OB的长，从而可以求得OA的长．
解答 解：由数轴可得，
OB的长度是：$\sqrt{（-2）^{2}+{1}^{2}}=\sqrt{5}$，
∵OA=OB，
∴OA=$\sqrt{5}$，
∵点A在原点的左侧，
∴数轴上点A表示的数是-$\sqrt{5}$，
故答案为：-$\sqrt{5}$．
点评 本题考查实数与数轴，解答本题的关键是求出OB的长，利用勾股定理的知识解答．
练习册系列答案
口算题天天练系列答案
相关题目
4．阿信、小怡两人打算搭乘同一班次电车上学，若此班次电车共有5节车厢，且阿信从任意一节车厢上车的机会相等，小怡从任意一节车厢上车的机会相等，则两人从同一节车厢上车的概率为何（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{5}$ | C． | $\frac{1}{10}$ | D． | $\frac{1}{25}$ |
5．
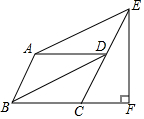如图，在?ABCD中，∠BAD=120°，连接BD，作AE∥BD交CD延长线于点E，过点E作EF⊥BC交BC的延长线于点F，且CF=1，则AB的长是（ ）
如图，在?ABCD中，∠BAD=120°，连接BD，作AE∥BD交CD延长线于点E，过点E作EF⊥BC交BC的延长线于点F，且CF=1，则AB的长是（ ）| A． | 2 | B． | 1 | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |
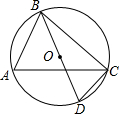如图，⊙O的直径BD=4，∠A=60°，则CD的长度为2．
如图，在?ABCD中，直线EF∥BD，并且与CD、CB的延长线分别交于E、F，交AD于M，交AB于N．求证：EN=FM．