题目内容
17.如果一个直角三角形的三条边的长度为6,8,a,则a=10或2$\sqrt{7}$.分析 本题已知直角三角形的两边长,但未明确这两条边是直角边还是斜边,因此两条边中的较长边8既可以是直角边,也可以是斜边,所以求第三边的长必须分类讨论,即8是斜边或直角边的两种情况,然后利用勾股定理求解.
解答 解:设第三边为a,
(1)若8是直角边,则第三边a是斜边,由勾股定理得:
62+82=a2,
∴a=10;
(2)若8是斜边,则第三边a为直角边,由勾股定理得:
62+a2=82,
∴x=2$\sqrt{7}$;
∴第三边的长为10或2$\sqrt{7}$.
故答案为:10或2$\sqrt{7}$.
点评 本题考查了利用勾股定理解直角三角形的能力,当已知条件中没有明确哪是斜边时,要注意讨论,一些学生往往忽略这一点,造成丢解.

练习册系列答案
相关题目
16.2017年5月5日,国产大飞机C919首飞圆满成功.C919大型客机是我国首次按照国际适航标准研制的150座级干线客机,首飞成功标志着我国大型客机项目取得重大突破,是我国民用航空工业发展的重要里程碑.目前,C919大型客机已有国内外多家客户预订六百架 表1是其中20家客户的订单情况.
表1
根据表1所提供的数据补全表2,并求出这组数据的中位数和众数.
表2
表1
| 客户 | 订单(架) | 客户 | 订单(架) |
| 中国国际航空 | 20 | 工银金融租赁有限公司 | 45 |
| 中国东方航空 | 20 | 平安国际融资租赁公司 | 50 |
| 中国南方航空 | 20 | 交银金融租赁有限公司 | 30 |
| 海南航空 | 20 | 中国飞机租赁有限公司 | 20 |
| 四川航空 | 15 | 中银航空租赁私人有限公司 | 20 |
| 河北航空 | 20 | 农银金融租赁有限公司 | 45 |
| 幸福航空 | 20 | 建信金融租赁股份有限公司 | 50 |
| 国银金融租赁有限公司 | 15 | 招银金融租赁公司 | 30 |
| 美国通用租赁公司GECAS | 20 | 兴业金融租赁公司 | 20 |
| 泰国都市航空 | 10 | 德国普仁航空公司 | 7 |
表2
| 订单(架) | 7 | 10 | 15 | 20 | 30 | 50 | |
| 客户(家) | 1 | 1 | 2 | 2 | 2 |
 如图所示,已知OA=OB,则数轴上点A表示的数是-$\sqrt{5}$.
如图所示,已知OA=OB,则数轴上点A表示的数是-$\sqrt{5}$.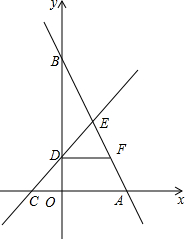 如图,直线y=kx+b分别与x轴、y轴交于点A(2,0)和点B,直线y=x+1分别与x轴、y轴交于点C和点D,两直线交于第一象限内的点E,并且点D为CE的中点.
如图,直线y=kx+b分别与x轴、y轴交于点A(2,0)和点B,直线y=x+1分别与x轴、y轴交于点C和点D,两直线交于第一象限内的点E,并且点D为CE的中点.