题目内容
5.先将(1-$\frac{1}{x}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$化简,再从1,0,-1,2中任选一个你认为合适的代数代入并求值.分析 先对原式进行化简,然后取x=2代入求值即可解答本题.
解答 解:(1-$\frac{1}{x}$)÷$\frac{{x}^{2}-2x+1}{{x}^{2}-1}$
=$\frac{x-1}{x}×\frac{(x+1)(x-1)}{(x-1)^{2}}$
=$\frac{x+1}{x}$,
当x=2时,原式=$\frac{2+1}{2}=\frac{3}{2}$.
点评 本题考查分式的化简求值,解题的关键是明确题意,发现题目中隐含的条件,题目中说从1,0,-1,2中任选一个你认为合适的代数代入并求值,这其中如果x取1,0,-1中的任何一个数时,原式都无意义,只有取2时,原式才有意义.

练习册系列答案
相关题目
16.绝对值为$\sqrt{3}$的数是( )
| A. | $\sqrt{3}$ | B. | $±\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $±\frac{\sqrt{3}}{3}$ |
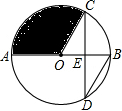 如图,AB是⊙O的直径,弦CD交AB于点E,且E是CD的中点,∠CDB=30°,CD=6$\sqrt{3}$,则阴影部分面积为( )
如图,AB是⊙O的直径,弦CD交AB于点E,且E是CD的中点,∠CDB=30°,CD=6$\sqrt{3}$,则阴影部分面积为( )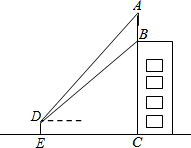 如图,某建筑物BC顶部接收塔AB,且点A,B,C在同一条直线上,小明在D处观接收塔顶部A的仰角为45°,观测旗杆底部B的仰角为30°.已知点D到地面的距离DE为1.7m,EC=30m,求接收塔AB的高度和建筑物BC的高度(结果保留根号).
如图,某建筑物BC顶部接收塔AB,且点A,B,C在同一条直线上,小明在D处观接收塔顶部A的仰角为45°,观测旗杆底部B的仰角为30°.已知点D到地面的距离DE为1.7m,EC=30m,求接收塔AB的高度和建筑物BC的高度(结果保留根号).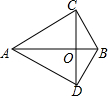 如图,△ABC中,∠ACB=90°,∠BAC=30°,将线段AC绕点A顺时针旋转60°得到线段AD,连接CD交AB于点O,连接BD.
如图,△ABC中,∠ACB=90°,∠BAC=30°,将线段AC绕点A顺时针旋转60°得到线段AD,连接CD交AB于点O,连接BD.