题目内容
13.某商场销售A、B两种品牌的节能灯,每盏售价B种节能灯比A种节能灯多10元,且花费150元购买A种节能灯与花费200元购买B种节能灯的数量相同.(1)求每盏A、B两种品牌的节能灯的售价分别是多少元?
(2)某公司准备在该商场从A、B两种品牌的节能灯中选购其中一种,购买数量不少于10盏,因为购买数量较多,商场可给予以下优惠:购买A种节能灯每盏均按原售价8折优惠;购买B种节能灯,5盏按原售价付款,超出5盏每盏按原售价5折优惠,请帮助该公司判断购买哪种节能灯更省钱.
分析 (1)设每盏A种品牌的节能灯的售价是x元,则每盏B种品牌的节能灯的售价是(x+10)元,根据“花费150元购买A种节能灯与花费200元购买B种节能灯的数量相同”列出方程,求解即可;
(2)设该公司购买节能灯a盏,则a≥10.用含a的代数式分别表示出购买A种品牌的节能灯的费用为:30×0.8a=24a(元);购买B种品牌的节能灯的费用为:40×5+40×0.5(a-5)=20a+100(元).再分三种情况讨论即可求解.
解答 解:(1)设每盏A种品牌的节能灯的售价是x元,则每盏B种品牌的节能灯的售价是(x+10)元,
根据题意得$\frac{150}{x}$=$\frac{200}{x+10}$,
解得x=30,
经检验,x=30是原方程的解.
则x+10=40.
答:每盏A种品牌的节能灯的售价是30元,每盏B种品牌的节能灯的售价是40元;
(2)设该公司购买节能灯a盏,则a≥10.
如果购买A种品牌的节能灯,那么费用为:30×0.8a=24a(元);
如果购买B种品牌的节能灯,那么费用为:40×5+40×0.5(a-5)=20a+100(元).
当24a=20a+100时,a=25;
当24a>20a+100时,a>25;
当24a<20a+100时,a<25.
故该公司购买节能灯盏数a满足10≤a<25时,购买A种品牌的节能灯更省钱;
购买节能灯25盏时,两种品牌的节能灯一样省钱;
购买节能灯盏数a满足a>25时,购买B种品牌的节能灯更省钱.
点评 本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
1.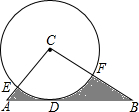 如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )
 如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )
如图,在Rt△ABC中,∠C=90°,∠B=30°,以点C为圆心,4为半径的⊙C与AB相切于点D,交CA于E,交CB于F,则图中阴影部分的面积为( )| A. | $\frac{32}{3}\sqrt{3}-4π$ | B. | $\frac{32}{3}\sqrt{3}-2π$ | C. | 16-4π | D. | 16-2π |
18.方程x2-5x=0的解是( )
| A. | x1=x2=5 | B. | x1=x2=0 | C. | x1=0,x2=5 | D. | x1=-5,x2=0 |
2.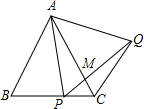 如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
①AB∥CQ;②∠ACQ=60°;③AP2=AM•AC;④若BP=PC,则PQ⊥AC.
 如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )①AB∥CQ;②∠ACQ=60°;③AP2=AM•AC;④若BP=PC,则PQ⊥AC.
| A. | 只有①② | B. | 只有①③ | C. | 只有①②③ | D. | ①②③④ |
3.已知:2m+3n=5,则4m•8n=( )
| A. | 16 | B. | 25 | C. | 32 | D. | 64 |
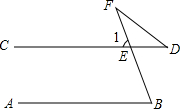 如图,AB∥CD,∠B=78°,∠D=32°,求∠F的度数.
如图,AB∥CD,∠B=78°,∠D=32°,求∠F的度数. 如图,边长等于4的正方形ABCD两个顶点A与D分别在x轴和y轴上滑动(A、D都不与坐标原点O重合),作CE⊥x轴,垂足为E,当OA等于2$\sqrt{2}$时,四边形OACE面积最大.
如图,边长等于4的正方形ABCD两个顶点A与D分别在x轴和y轴上滑动(A、D都不与坐标原点O重合),作CE⊥x轴,垂足为E,当OA等于2$\sqrt{2}$时,四边形OACE面积最大.