题目内容
17.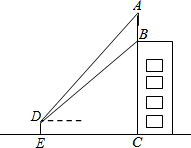 如图,某建筑物BC顶部接收塔AB,且点A,B,C在同一条直线上,小明在D处观接收塔顶部A的仰角为45°,观测旗杆底部B的仰角为30°.已知点D到地面的距离DE为1.7m,EC=30m,求接收塔AB的高度和建筑物BC的高度(结果保留根号).
如图,某建筑物BC顶部接收塔AB,且点A,B,C在同一条直线上,小明在D处观接收塔顶部A的仰角为45°,观测旗杆底部B的仰角为30°.已知点D到地面的距离DE为1.7m,EC=30m,求接收塔AB的高度和建筑物BC的高度(结果保留根号).
分析 过点D作DF⊥AC于F,根据正切的概念分别求出AF、BF,结合图形计算即可.
解答 解:过点D作DF⊥AC于F,
由题意得,DE=1.7,EC=30,∠ACE=90°,∠DEC=90°,
∴四边形DECF是矩形,
∴DF=EC=30,FC=DE=1.7,
在Rt△DFA中,tan∠ADF=$\frac{AF}{DF}$,
∴AF=DF•tan∠ADF=30,
在Rt△DFB中,tan∠BDF=$\frac{BF}{DF}$,
∴BF=DF•tan∠BDF=10$\sqrt{3}$,
则AB=AF-BF=(30-10$\sqrt{3}$)m;
BC=BF+FC=(10$\sqrt{3}$+1.7)m.
答:接收塔AB的高度是(30-10$\sqrt{3}$)m,建筑物BC的高度为(10$\sqrt{3}$+1.7)m.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
2.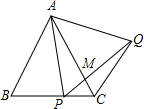 如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
①AB∥CQ;②∠ACQ=60°;③AP2=AM•AC;④若BP=PC,则PQ⊥AC.
 如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
如图,在△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )①AB∥CQ;②∠ACQ=60°;③AP2=AM•AC;④若BP=PC,则PQ⊥AC.
| A. | 只有①② | B. | 只有①③ | C. | 只有①②③ | D. | ①②③④ |
6.在平面直角坐标系中,点P(-3,2)关于直线y=x对称点的坐标是( )
| A. | (-3,-2) | B. | (3,2) | C. | (2,-3) | D. | (3,-2) |
7.今年国庆黄金周,南部山区农家乐共接待15.8万游客,把15.8万用科学记数法表示为( )
| A. | 1.58×105 | B. | 1.58×l04 | C. | 158×103 | D. | 0.158×106 |
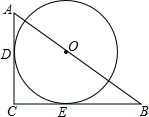 如图,⊙O与Rt△ACB的两直角边AC、BC相切,切点分别为D、E两点,且圆心O在斜边AB上.
如图,⊙O与Rt△ACB的两直角边AC、BC相切,切点分别为D、E两点,且圆心O在斜边AB上. 如图,已知一次函数y=kx+b的图象与x轴交于点(3,0),与y轴交于点(0,2),不等式kx+b≥2解集是x≤0.
如图,已知一次函数y=kx+b的图象与x轴交于点(3,0),与y轴交于点(0,2),不等式kx+b≥2解集是x≤0.