题目内容
10．咸阳市某奶粉企业，每天生产幼儿Ⅰ段和Ⅱ段奶粉共800罐，Ⅰ段和Ⅱ段的成本和利润如下表，设每天生产Ⅰ段奶粉x罐，每天获利y元．（1）请写出y关于x的函数关系式；
（2）如果该奶粉企业每天至少投入成本50000元，那么每天最多获利多少元．
| Ⅰ | Ⅱ | |
| 成本（元/瓶） | 60 | 70 |
| 利润（元/瓶） | 30 | 20 |
分析 （1）每天生产Ⅰ段奶粉x罐，则每天生产Ⅱ段奶粉（800-x）罐，根据：Ⅰ段奶粉利润+Ⅱ段奶粉利润=总利润，列出函数关系式即可；
（2）根据：Ⅰ段奶粉总成本+Ⅱ段奶粉总成本≥50000，求出x的取值范围，结合一次函数性质可得利润的最大值．
解答 解：（1）根据题意，得：y=30x+20（800-x）=10x+16000；
（2）由题意，知：60x+70（80-x）≥50000，
解得：x≤600，
由（1）y=10x+16000知，y随x的增大而增大，
则当x=600时，y取最大值，y最大值=10×600+16000=22000（元），
答：每天至多获利22000元．
点评 本题主要考查一次函数的实际应用能力，根据题意抓住相等关系列出函数关系式是解题的根本和关键，由不等关系求得x的取值范围是求最值的条件．
练习册系列答案
相关题目
20．
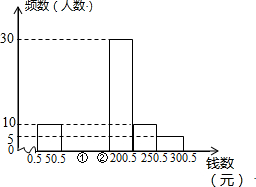某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量（钱数取整数元），以便引导学生树立正确的消费观．根据调查数据制成频数分布表和频数分布直方图．
（1）补全频数分布表和直方图；
（2）研究所认为，应对消费150元以上的学生提出勤俭节约的建议，试估计应对该校4000名学生中约多少名学生提出这项建议？
某青少年研究所随机调查了某校100名学生寒假中花费零花钱的数量（钱数取整数元），以便引导学生树立正确的消费观．根据调查数据制成频数分布表和频数分布直方图．（1）补全频数分布表和直方图；
（2）研究所认为，应对消费150元以上的学生提出勤俭节约的建议，试估计应对该校4000名学生中约多少名学生提出这项建议？
| 分 组 | 频数 | 所占比例 |
| 0.5～50.5 | 10 | 0.1 |
| 50.5～100.5 | 20 | 0.2 |
| 100.5～150.5 | 35 | 35 |
| 150.5～200.5 | 30 | 0.3 |
| 200.5～250.5 | 10 | 0.1 |
| 250.5～300.5 | 5 | 0.05 |
| 合 计 | 100 | ------ |
1．
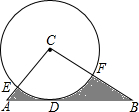如图，在Rt△ABC中，∠C=90°，∠B=30°，以点C为圆心，4为半径的⊙C与AB相切于点D，交CA于E，交CB于F，则图中阴影部分的面积为（ ）
如图，在Rt△ABC中，∠C=90°，∠B=30°，以点C为圆心，4为半径的⊙C与AB相切于点D，交CA于E，交CB于F，则图中阴影部分的面积为（ ）| A． | $\frac{32}{3}\sqrt{3}-4π$ | B． | $\frac{32}{3}\sqrt{3}-2π$ | C． | 16-4π | D． | 16-2π |
18．方程x2-5x=0的解是（ ）
| A． | x1=x2=5 | B． | x1=x2=0 | C． | x1=0，x2=5 | D． | x1=-5，x2=0 |
平面上，将边长相等的正三角形、正方形、正六边形的一边重合并叠在一起，如图，则∠1+∠2+∠3=60°．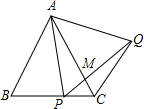
如图，在△ABC为等边三角形，P为BC上一点，△APQ为等边三角形，PQ与AC相交于点M，则下列结论中正确的是（ ）
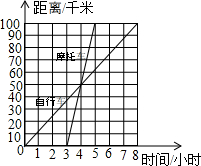如图所示，是一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的图象，两地间的距离是100千米，请根据图象填空：