题目内容
15.已知a=4,b,c是方程x2-5x+6=0的两个根,则以a、b、c为三边的三角形面积是$\frac{3\sqrt{15}}{4}$.分析 先利用因式分解法解方程得到b、c的值为2、3,如图,△ABC中,AB=2,AC=3,BC=4,作AD⊥BC于D,设BD=x,则CD=4-x,利用勾股定理得到22-x2=32-(4-x)2,解得x=$\frac{11}{8}$,则可计算出AD的长,然后根据三角形面积公式求解.
解答 解:x2-5x+6=0,
(x-2)(x-3)=0,
x-2=0或x-3=0,
所以x1=2,x2=3,
如图,△ABC中,AB=2,AC=3,BC=4,作AD⊥BC于D,设BD=x,则CD=4-x,
在Rt△ABD中,AD2=AB2-BD2=22-x2,
在Rt△ACD中,AD2=AC2-CD2=32-(4-x)2,
22-x2=32-(4-x)2,解得x=$\frac{11}{8}$,
所以AD=$\sqrt{{2}^{2}-(\frac{11}{8})^{2}}$=$\frac{3\sqrt{15}}{8}$,
所以△ABC的面积=$\frac{1}{2}$×4×$\frac{3\sqrt{15}}{8}$=$\frac{3\sqrt{15}}{4}$.
故答案为$\frac{3\sqrt{15}}{4}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了三角形面积公式.

练习册系列答案
相关题目
6.在平面直角坐标系中,点P(-3,2)关于直线y=x对称点的坐标是( )
| A. | (-3,-2) | B. | (3,2) | C. | (2,-3) | D. | (3,-2) |
3.已知:2m+3n=5,则4m•8n=( )
| A. | 16 | B. | 25 | C. | 32 | D. | 64 |
10.某剧院的观众席的座位为扇形,且按下列方式设置:
(1)按照上表所示的规律,当x每增加1时,y如何变化?
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
| 排数(x) | 1 | 2 | 3 | 4 | … |
| 座位数(y) | 50 | 53 | 56 | 59 | … |
(2)写出座位数y与排数x之间的关系式;
(3)按照上表所示的规律,某一排可能有90个座位吗?说说你的理由.
7.今年国庆黄金周,南部山区农家乐共接待15.8万游客,把15.8万用科学记数法表示为( )
| A. | 1.58×105 | B. | 1.58×l04 | C. | 158×103 | D. | 0.158×106 |
4.计算:(-2a)2•(-3a)3的结果是( )
| A. | -108a5 | B. | -108a6 | C. | 108a5 | D. | 108a6 |
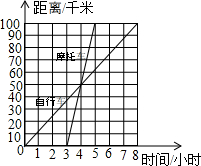 如图所示,是一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的图象,两地间的距离是100千米,请根据图象填空:
如图所示,是一骑自行车者与一骑摩托车者沿相同路线由甲地到乙地行驶过程的图象,两地间的距离是100千米,请根据图象填空: