题目内容
 已知,如图所示,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.
已知,如图所示,AB=AC,BD=CD,DE⊥AB于点E,DF⊥AC于点F,求证:DE=DF.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:连接AD,利用SSS得到三角形ABD与三角形ACD全等,利用全等三角形对应角相等得到∠EAD=∠FAD,即AD为角平分线,再由DE⊥AB,DF⊥AC,利用角平分线定理即可得证.
解答: 证明:连接AD,
证明:连接AD,
在△ACD和△ABD中,
,
∴△ACD≌△ABD(SSS),
∴∠EAD=∠FAD,即AD平分∠EAF,
∵DE⊥AE,DF⊥AF,
∴DE=DF.
 证明:连接AD,
证明:连接AD,在△ACD和△ABD中,
|
∴△ACD≌△ABD(SSS),
∴∠EAD=∠FAD,即AD平分∠EAF,
∵DE⊥AE,DF⊥AF,
∴DE=DF.
点评:此题考查了全等三角形的判定与性质,以及角平分线定理,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
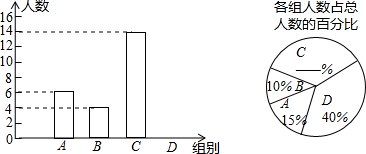
某种正方形合金板材的成本y(元)与它的面积成正比,设边长为x厘米.当x=3时,y=18,那么当成本为72元时,边长为( )
| A、6厘米 | B、12厘米 |
| C、24厘米 | D、36厘米 |
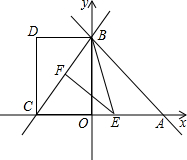 如图,在平面直角坐标系xoy中,直线
如图,在平面直角坐标系xoy中,直线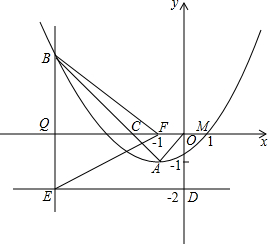 如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴交点M(1,0).C为x轴上一点,且∠CAO=90°,线段AC的延长线交抛物线于B点,另有点F(-1,0).
如图,抛物线y=ax2+bx+c(a≠0)的顶点为A(-1,-1),与x轴交点M(1,0).C为x轴上一点,且∠CAO=90°,线段AC的延长线交抛物线于B点,另有点F(-1,0). 小明听说“武黄城际列车”已经开通,便设计了如下问题:如图,以往从黄石A坐客车到武昌客运站B,现在可以在A坐城际列车到武汉青山站C,再从青山站C坐市内公共汽车到武昌客运站B.设AB=80km,BC=20km,∠ABC=120°.请你帮助小明解决以下问题:
小明听说“武黄城际列车”已经开通,便设计了如下问题:如图,以往从黄石A坐客车到武昌客运站B,现在可以在A坐城际列车到武汉青山站C,再从青山站C坐市内公共汽车到武昌客运站B.设AB=80km,BC=20km,∠ABC=120°.请你帮助小明解决以下问题: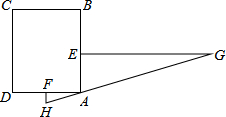 “今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=
“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》,意思是说:如图,矩形ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB,AD的中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=