题目内容
16．
如图，在△ABC中，∠C=90°，∠B=30°，AD平分∠CAB，如果BD=12cm，那么CD的长应为6cm；点D到AB的距离是6cm．
分析 作DE⊥AB于E，根据角平分线的性质得到DC=DE，根据直角三角形的性质求出DE，得到答案．
解答 解：
作DE⊥AB于E，
∵AD平分∠CAB，DE⊥AB，∠C=90°，
∴DC=DE，
∵∠B=30°，DE⊥AB，
∴DE=$\frac{1}{2}$BD=6cm，
∴DC=6cm，
故答案为：6；6．
点评 本题考查的是直角三角形的性质、角平分线的性质，掌握直角三角形中，30°角所对的直角边等于斜边的一半是解题的关键．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
11．
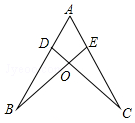如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，有下列条件：①AB=AC；②DC=BE；③∠B=∠C，从中选择两个条件判定△ABE≌△ACD，是真命题的个数为（ ）
如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，有下列条件：①AB=AC；②DC=BE；③∠B=∠C，从中选择两个条件判定△ABE≌△ACD，是真命题的个数为（ ）| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
1．下列判断错误的是（ ）
| A． | 当a≠0时，分式$\frac{2}{a}$有意义 | B． | 当a=-3时，分式$\frac{a+3}{{{a^2}-9}}$有意义 | ||
| C． | 当$a=-\frac{1}{2}$时，分式$\frac{2a+1}{a}$的值为0 | D． | 当a=1时，分式$\frac{2a-1}{a}$的值为1 |
8．
如图，哪一个图形是左面正方体的展开图（ ）
如图，哪一个图形是左面正方体的展开图（ ）| A． |  | B． |  | C． |  | D． |  |
5．
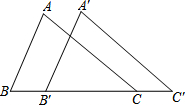如图，在△ABC中，AB=8，BC=12，∠B=60°，将△ABC沿着射线BC的方向平移4个单位后，得到△A'B'C'，连接AC，则△A'B'C的面积是（ ）
如图，在△ABC中，AB=8，BC=12，∠B=60°，将△ABC沿着射线BC的方向平移4个单位后，得到△A'B'C'，连接AC，则△A'B'C的面积是（ ）| A． | 16 | B． | $4\sqrt{3}$ | C． | $16\sqrt{3}$ | D． | $32\sqrt{3}$ |