题目内容
4.某中学为开拓学生视野,开展“课外读书周”活动,活动后期随机调查了八年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图的信息回答下列问题: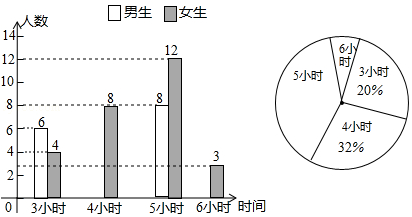
(1)本次调查的学生总数为50人;
(2)请你补全条形统计图;
(3)在扇形统计图中,课外阅读时间为5小时的扇形的圆心角度数是144°;
(4)若全校八年级共有学生700人,估计八年级一周课外阅读时间为6小时的学生有多少人?
分析 (1)根据统计图可知,课外阅读达3小时的共10人,占总人数的20%,由此可得出总人数;
(2)求出课外阅读时间4小时与6小时男生的人数,补全条形统计图即可;
(3)求出课外阅读时间为5小时的人数,再求出其人数与总人数的比值即可得出扇形的圆心角度数;
(4)求出总人数与课外阅读时间为6小时的学生人数的百分比的积即可.
解答 解:(1)本次调查的学生总数为$\frac{6+4}{20%}$=50人,
故答案为:50.
(2)∵课外阅读4小时的人数是32%,
∴50×32%=16(人),
∴男生人数=16-8=8(人);
∴课外阅读6小时的人数=50-6-4-8-8-8-12-3=1(人),
如图所示.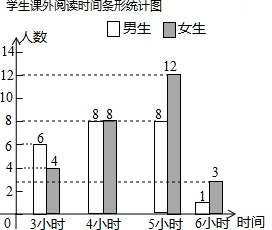
(3)∵课外阅读5小时的人数是20人,
∴$\frac{20}{50}$×360°=144°.
故答案为:144°;
(4)∵课外阅读5小时的人数是4人,
∴700×$\frac{4}{50}$=56(人).
答:八年级一周课外阅读时间为6小时的学生大约有56人.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
19.下列计算中,正确的是( )
| A. | $\sqrt{25}=±5$ | B. | $\sqrt{(-7)^{2}=-7}$ | C. | |4-3$\sqrt{2}$|=3$\sqrt{2}$-4 | D. | ($\sqrt{2}+1$)2=3 |
9.计算-2x(x2-1)的结果是( )
| A. | -2x3-2x | B. | -2x3+x | C. | -2x3+2x | D. | -x3+2x |
13.下列说法错误的是( )
| A. | 过一点能作无数条直线 | |
| B. | 连接两点之间的线段就是两点间的距离 | |
| C. | 反向延长线段AB和延长线段BA是一回事 | |
| D. | 两点确定一条直线 |
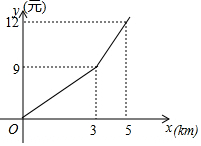 某出租车公司的收费标准如图,其中x(km)表示行驶里程,y(元)表示车费,若乘客在打车后付费42元,则该乘客乘坐出租车行驶了25km.
某出租车公司的收费标准如图,其中x(km)表示行驶里程,y(元)表示车费,若乘客在打车后付费42元,则该乘客乘坐出租车行驶了25km. 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,如果BD=12cm,那么CD的长应为6cm;点D到AB的距离是6cm.
如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,如果BD=12cm,那么CD的长应为6cm;点D到AB的距离是6cm. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(3,-1).以原点O为对称中心,画出△ABC关于原点O对称的△A′B′C′,并写出A′、B′、C′的坐标.
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(3,-1).以原点O为对称中心,画出△ABC关于原点O对称的△A′B′C′,并写出A′、B′、C′的坐标.