题目内容
7.已知在△ABC中,三边长a,b,c满足a2+2b2+c2-2ab-2bc=0,请判断△ABC的形状并证明你的结论.分析 由a2+2b2+c2-2ab-2bc=0分组因式分解,利用非负数的性质得到三边关系,从而判定三角形形状.
解答 解:△ABC是等边三角形.
证明如下:
因为a2+2b2+c2-2ab-2bc=0,
所以a2-2ab+b2+b2-2bc+c2=0,
(a-b)2+(b-c)2=0,
所以(a-b)2=0,(b-c)2=0,
得a=b且b=c,
即a=b=c,
所以△ABC是等边三角形.
点评 此题是一道把等边三角形的判定、因式分解和非负数的性质结合求解的综合题.考查学生综合运用数学知识的能力.

练习册系列答案
相关题目
4.以下说法正确的是( )
| A. | 有理数与数轴上的点一一对应 | |
| B. | 两个无理数的积一定是无理数 | |
| C. | 负数没有平方根也没有立方根 | |
| D. | 算术平方根等于它本身的数只有0或1 |
19.下列计算中,正确的是( )
| A. | $\sqrt{25}=±5$ | B. | $\sqrt{(-7)^{2}=-7}$ | C. | |4-3$\sqrt{2}$|=3$\sqrt{2}$-4 | D. | ($\sqrt{2}+1$)2=3 |
17.如果一个角的补角是150°,那么这个角的余角的度数是( )
| A. | 60° | B. | 30° | C. | 90° | D. | 120° |
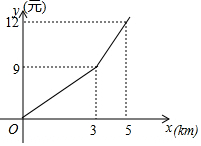 某出租车公司的收费标准如图,其中x(km)表示行驶里程,y(元)表示车费,若乘客在打车后付费42元,则该乘客乘坐出租车行驶了25km.
某出租车公司的收费标准如图,其中x(km)表示行驶里程,y(元)表示车费,若乘客在打车后付费42元,则该乘客乘坐出租车行驶了25km. 如图,AC平分∠BAD,CD⊥AD于点D,AB=2AD,求证:AC=BC.
如图,AC平分∠BAD,CD⊥AD于点D,AB=2AD,求证:AC=BC. 如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,如果BD=12cm,那么CD的长应为6cm;点D到AB的距离是6cm.
如图,在△ABC中,∠C=90°,∠B=30°,AD平分∠CAB,如果BD=12cm,那么CD的长应为6cm;点D到AB的距离是6cm.