题目内容
已知圆锥的体积V=
Sh,当h=5cm时,底面积S为30cm2.
(1)当圆锥的体积不变时,求S关于h的函数解析式;
(2)求当高h=10cm时的底面积S;
(3)画出S关于h的函数图象,求当h为何值时,S<50cm2.
| 1 |
| 3 |
(1)当圆锥的体积不变时,求S关于h的函数解析式;
(2)求当高h=10cm时的底面积S;
(3)画出S关于h的函数图象,求当h为何值时,S<50cm2.
考点:反比例函数的应用
专题:
分析:(1)首先根据已知求出V的值,进而代入V=
Sh即可求得S关于h的函数解析式;
(2)代入h=10cm求得底面积S即可;
(3)根据h的取值范围作出图象,利用图象回答当h为何值时,S<50cm2即可.
| 1 |
| 3 |
(2)代入h=10cm求得底面积S即可;
(3)根据h的取值范围作出图象,利用图象回答当h为何值时,S<50cm2即可.
解答:解:(1)∵V=
Sh,当h为5cm时,底面积为30,
∴V=
×5×30=50(cm3),
∴50=
sh,
∴s关于h的函数解析式为:s=
;
(2)当h=10cm时,S=
=15cm2;
(3)∵h>0,
所以图象为:

∴当0<x<3时,S<50cm2.
| 1 |
| 3 |
∴V=
| 1 |
| 3 |
∴50=
| 1 |
| 3 |
∴s关于h的函数解析式为:s=
| 150 |
| h |
(2)当h=10cm时,S=
| 150 |
| 10 |
(3)∵h>0,
所以图象为:

∴当0<x<3时,S<50cm2.
点评:本题考查了反比例函数的应用,解题的关键是根据题意求得反比例函数的解析式.

练习册系列答案
相关题目
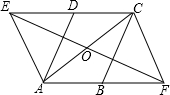 如图,在平行四边形ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.求证:四边形AFCE是平行四边形.
如图,在平行四边形ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.求证:四边形AFCE是平行四边形. 如图,已知CD垂直平分AB,AB平分∠CAD.求证:AD∥BC.
如图,已知CD垂直平分AB,AB平分∠CAD.求证:AD∥BC.
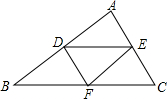 如图,点D,E,F分别是△ABC三边上的中点,若AB=10cm,AC=8cm,BC=12cm,则EF=
如图,点D,E,F分别是△ABC三边上的中点,若AB=10cm,AC=8cm,BC=12cm,则EF=