题目内容
3．因式分解：（1）2（x+y）2z2-4（x-y）z2-48z2
（2）81（x+y）4-16（x-y）4．
分析 （1）原式提取公因式即可得到结果；
（2）原式利用平方差公式分解即可．
解答 解：（1）原式=2z2[（x+y）2-2（x-y）-24]；
（2）原式=[9（x+y）2+4（x-y）2][9（x+y）2-4（x-y）2]
=[9（x+y）2+4（x-y）2][3（x+y）+2（x-y）][3（x+y）-2（x-y）]
=（13x2+10xy+13y2）（5x+y）（x+5y）．
点评 此题考查了提公因式与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
11．
在同一坐标系中画出下列函数的图象：
（1）y=-x2；
（2）y=-（x+2）2
（3）y=-（x-1）2
在同一坐标系中画出下列函数的图象：（1）y=-x2；
（2）y=-（x+2）2
（3）y=-（x-1）2
| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y=-x2 | … | … | |||||||||
| y=-（x+2）2 | … | … | |||||||||
| y=-（x-1）2 | … | … |
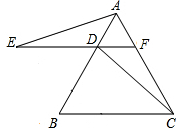如图，△ABC是等边三角形，过AB上的一点D作DF∥BC，交AC于F，在FD的延长线上取点E，使DE=DB，连接AE、CD．证明：△AFE≌△DAC．
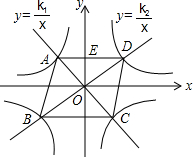如图，经过O的直线AC，BD分别与反比例函数y=$\frac{{k}_{1}}{x}$（k1＜0），y=$\frac{{k}_{2}}{x}$（k＞0）相交于点A，C，B，D，且AC⊥BD