Question

8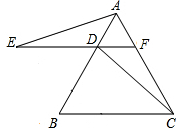．如图，△ABC是等边三角形，过AB上的一点D作DF∥BC，交AC于F，在FD的延长线上取点E，使DE=DB，连接AE、CD．证明：△AFE≌△DAC．

Answer 1

分析 根据等边三角形的性质可得∠BAC=∠ACB=60°，AC=AB=AB，再证明∠AFD=∠ACB=60°，EF=AC，然后利用SAS定理判定△AFE≌△DAC即可．

解答 证明：∵△ABC是等边三角形，
∴∠BAC=∠ACB=60°，AC=AB=AB，
∵DF∥BC，
∴∠AFD=∠ACB=60°，
∴△ADF是等边三角形，
∴AF=DF=AD，
∴FC=DB，
∵DE=DB，
∴EF=AC，
在△AEF和△DCA中，$\left\{\begin{array}{l}{AD=AF}\\{∠DAF=∠AFD}\\{EF=AC}\end{array}\right.$，
∴△AFE≌△DAC（SAS）．

点评 此题考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．