题目内容
某工程队承包了某标段全长1957米的过江隧道施工任务,甲、乙两个班组分别从南、北两端同时掘进.已知甲组比乙组平均每天多掘进0.5米,经过6天施工,两组共掘进了57米.
(1)求甲、乙两班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进0.3米,乙组平均每天能比原来多掘进0.2米.按此施工进度,能够比原来少用多少天完成任务?
(1)求甲、乙两班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进0.3米,乙组平均每天能比原来多掘进0.2米.按此施工进度,能够比原来少用多少天完成任务?
考点:一元一次方程的应用
专题:
分析:(1)设甲班组平均每天掘进x米,则乙班组平均每天掘进(x-0.5)米,根据已知经过6天施工,两组共掘进了57米的关系列方程组求解.
(2)由(1)和在剩余的工程中,甲组平均每天能比原来多掘进0.3米,乙组平均每天能比原来多掘进0.2米分别求出按原来进度和现在进度的天数,即求出少用天数.
(2)由(1)和在剩余的工程中,甲组平均每天能比原来多掘进0.3米,乙组平均每天能比原来多掘进0.2米分别求出按原来进度和现在进度的天数,即求出少用天数.
解答:解:(1)设甲班组平均每天掘进x米,则乙班组平均每天掘进(x-0.5)米,依题意有
6x+6(x-0.5)=57
解得x=5.
x-0.5=4.5.
故甲班组平均每天掘进5米,乙班组平均每天掘进4.5米.
(2)设按原来的施工进度和改进施工技术后的进度分别还需a天,b天完成任务,则
a=(1957-57)÷(5+4.5)=200(天),
b=(1957-57)÷(5+0.3+4.5+0.2)=190(天),
∵a-b=10,
∴按此施工进度,能够比原来少用10天完成任务.
6x+6(x-0.5)=57
解得x=5.
x-0.5=4.5.
故甲班组平均每天掘进5米,乙班组平均每天掘进4.5米.
(2)设按原来的施工进度和改进施工技术后的进度分别还需a天,b天完成任务,则
a=(1957-57)÷(5+4.5)=200(天),
b=(1957-57)÷(5+0.3+4.5+0.2)=190(天),
∵a-b=10,
∴按此施工进度,能够比原来少用10天完成任务.
点评:此题考查的知识点是二元一次方程组的应用,解题的关键是根据已知找出相等关系列方程求解,然后由已知和所求原来进度求出少用天数.

练习册系列答案
相关题目
已知sinA=0.1782,则锐角A的度数大约为( )
| A、8° | B、9° | C、10° |
 如图,已知OC平分∠AOB,点P在OC上,以点P为圆心的⊙P与OA相切,那么是否也与OB相切?说明理由.
如图,已知OC平分∠AOB,点P在OC上,以点P为圆心的⊙P与OA相切,那么是否也与OB相切?说明理由.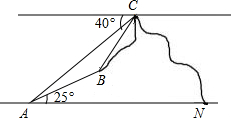 如图,MN表示水平地面,由地面上A处测得山上B处的仰角是25°,由山顶C处测得B处的俯角是40°.若AB:BC=2:3,求由A处测得C处的仰角(结果精确到0.1°).
如图,MN表示水平地面,由地面上A处测得山上B处的仰角是25°,由山顶C处测得B处的俯角是40°.若AB:BC=2:3,求由A处测得C处的仰角(结果精确到0.1°).