题目内容
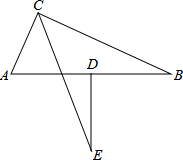 在△ABC中,已知AB=13,BC=12,CA=5,D为边AB的中点,DE⊥AB且与∠ACB的平分线交于点E,求DE的长.
在△ABC中,已知AB=13,BC=12,CA=5,D为边AB的中点,DE⊥AB且与∠ACB的平分线交于点E,求DE的长.考点:圆的综合题
专题:
分析:以点D为圆心,DA为半径作圆交直线DE于点F,连接CF,AF,BF,首先利用勾股定理的逆定理证明△ABC为直角三角形,进而可得∠FCB=∠ECB,即E和F点重合,再由直角三角形中斜边上的中线等于斜边的一半即可求出DE的长.
解答:解:以点D为圆心,DA为半径作圆交直线DE于点F,连接CF,AF,BF,
∵AB=13,BC=12,CA=5.
∴BC2+CA2=AB2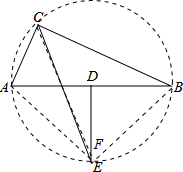 ,
,
∴△ABC为直角三角形,
∵DE⊥AB,
∴∠DBE=90°
∴∠FCB=
∠FDB=
×90°=45°,
∵CE平分∠ACB,
∴∠ECB=
∠ACB=45°,
∴∠FCB=∠ECB,
∵AB为圆的直径,
∴∠AEB=90°,
∴△AEB是直角三角形,
∴DE=DF=
AB=
.
∵AB=13,BC=12,CA=5.
∴BC2+CA2=AB2
 ,
,∴△ABC为直角三角形,
∵DE⊥AB,
∴∠DBE=90°
∴∠FCB=
| 1 |
| 2 |
| 1 |
| 2 |
∵CE平分∠ACB,
∴∠ECB=
| 1 |
| 2 |
∴∠FCB=∠ECB,
∵AB为圆的直径,
∴∠AEB=90°,
∴△AEB是直角三角形,
∴DE=DF=
| 1 |
| 2 |
| 13 |
| 2 |
点评:本题考查了勾股定理的逆定理的运用、圆周角定理的运用以及直角三角形中斜边上的中线等于斜边的一半性质的运用,题目的设计巧妙、新颖,解题的关键是正确添加辅助线构造直角三角形,是一道非常不错的中考题.

练习册系列答案
相关题目
已知a是一元二次方程x2-2x-3=0的一个实数根,则2a2-4a的值为( )
| A、-6 | B、6 | C、-2或6 |
 如图,已知OC平分∠AOB,点P在OC上,以点P为圆心的⊙P与OA相切,那么是否也与OB相切?说明理由.
如图,已知OC平分∠AOB,点P在OC上,以点P为圆心的⊙P与OA相切,那么是否也与OB相切?说明理由.