题目内容
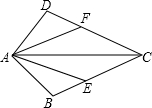 已知,如图,AB=AD,CE=CF,AC是∠DAB的平分线,求证:AE=AF.
已知,如图,AB=AD,CE=CF,AC是∠DAB的平分线,求证:AE=AF.考点:全等三角形的判定与性质
专题:证明题
分析:由AC是∠DAB的平分线就可以得出∠CAB=∠CAD,就可以得出△CAB≌△CAD,就可以得出∠ACB=∠ACD,进而可以得出△ACE≌△ACF,就可以得出结论.
解答:证明:∵AC是∠DAB的平分线,
∴∠CAB=∠CAD.
在△CAB和△CAD中,
,
∴△CAB≌△CAD(SAS),
∴∠ACB=∠ACD.
在△ACE和△ACF中,
,
∴△ACE≌△ACF(SAS),
∴AE=AF.
∴∠CAB=∠CAD.
在△CAB和△CAD中,
|
∴△CAB≌△CAD(SAS),
∴∠ACB=∠ACD.
在△ACE和△ACF中,
|
∴△ACE≌△ACF(SAS),
∴AE=AF.
点评:本题考查了角平分线的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
已知a是一元二次方程x2-2x-3=0的一个实数根,则2a2-4a的值为( )
| A、-6 | B、6 | C、-2或6 |
 如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=10cm,AB=8cm,求:
如图,折叠长方形的一边AD,使点D落在BC边上的点F处,BC=10cm,AB=8cm,求: 如图,已知OC平分∠AOB,点P在OC上,以点P为圆心的⊙P与OA相切,那么是否也与OB相切?说明理由.
如图,已知OC平分∠AOB,点P在OC上,以点P为圆心的⊙P与OA相切,那么是否也与OB相切?说明理由.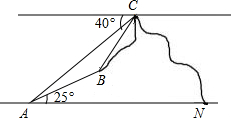 如图,MN表示水平地面,由地面上A处测得山上B处的仰角是25°,由山顶C处测得B处的俯角是40°.若AB:BC=2:3,求由A处测得C处的仰角(结果精确到0.1°).
如图,MN表示水平地面,由地面上A处测得山上B处的仰角是25°,由山顶C处测得B处的俯角是40°.若AB:BC=2:3,求由A处测得C处的仰角(结果精确到0.1°).