题目内容
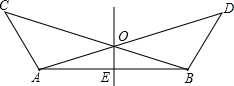 如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.
如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.(1)求证:△ABC≌△BAD;
(2)试判断OE和AB的位置关系,并给出证明.
考点:全等三角形的判定与性质
专题:
分析:(1)根据边角边判定全等三角形的方法即可求证△ABC≌△BAD;
(2)根据(1)中结论可得∠DAB=∠CBA,可得OA=OB,根据等腰三角形底边三线合一性质即可解题.
(2)根据(1)中结论可得∠DAB=∠CBA,可得OA=OB,根据等腰三角形底边三线合一性质即可解题.
解答:证明:(1)∵在△ABC和△BAD中
,
∴△ABC≌△BAD(SAS);
(2)OE⊥AB.
理由:∵△ABC≌△BAD,
∴∠DAB=∠CBA,
∴OA=OB,
∵点E是AB的中点,
∴OE⊥AB.
|
∴△ABC≌△BAD(SAS);
(2)OE⊥AB.
理由:∵△ABC≌△BAD,
∴∠DAB=∠CBA,
∴OA=OB,
∵点E是AB的中点,
∴OE⊥AB.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ABC≌△BAD是解题的关键.

练习册系列答案
相关题目
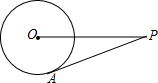 如图,P是⊙O外的一点,PA是⊙O的切线,若PO=13,PA=12,则⊙O的面积和周长分别为( )
如图,P是⊙O外的一点,PA是⊙O的切线,若PO=13,PA=12,则⊙O的面积和周长分别为( )| A、5π,10π |
| B、10π,5π |
| C、25π,10π |
| D、10π,25π |
 在平面直角坐标系xOy中,直线y=-
在平面直角坐标系xOy中,直线y=-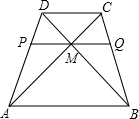 过梯形ABCD对角线的交点M,作底AB的平行线分别交两腰于P和Q,AP=2PD,求:图中的位似图形,并分别指出位似中心和位似比.
过梯形ABCD对角线的交点M,作底AB的平行线分别交两腰于P和Q,AP=2PD,求:图中的位似图形,并分别指出位似中心和位似比.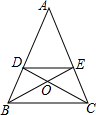 如图所示,在△ABC中,DE∥BC,AE:EC=2:1,则S△DOE:S△BOC=
如图所示,在△ABC中,DE∥BC,AE:EC=2:1,则S△DOE:S△BOC= 已知,如图,D为△ABC的边BC的中点,O为AD上的任一点,CD的延长线交AB于点E,BD的延长线交AC于点F,求证:EF∥BC.
已知,如图,D为△ABC的边BC的中点,O为AD上的任一点,CD的延长线交AB于点E,BD的延长线交AC于点F,求证:EF∥BC.