题目内容
已知，如图，D为△ABC的边BC的中点，O为AD上的任一点，CD的延长线交AB于点E，BD的延长线交AC于点F，求证：EF∥BC．考点：平行线分线段成比例
专题：证明题
分析：根据三角形面积公式易得S△ABD=S△ACD，S△BOD=S△COD，把它们相减即可得到S△ABO=S△ACO，再计算
=
=
，利用比例的性质得
，同理可得
=
，则
=
，然后根据如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边得到结论．
| AE |
| BE |
| S△ACE |
| S△BCE |
| S△AOE |
| S△BOE |
| AE |
| BE |
| S△AOC |
| S△BOC |
| AF |
| CF |
| S△AOB |
| S△BOC |
| AE |
| BE |
| AF |
| CF |
解答：证明：
∵D为△ABC的边BC的中点，
∴BD=CD，
∴S△ABD=S△ACD，S△BOD=S△COD，
∴S△ABO=S△ACO，
∵
=
=
=
=
，
同理可得
=
，
∴
=
，
∴EF∥BC．
∵D为△ABC的边BC的中点，∴BD=CD，
∴S△ABD=S△ACD，S△BOD=S△COD，
∴S△ABO=S△ACO，
∵
| AE |
| BE |
| S△ACE |
| S△BCE |
| S△AOE |
| S△BOE |
| S△ACE-S△AOE |
| S△BCE-S△BOE |
| S△AOC |
| S△BOC |
同理可得
| AF |
| CF |
| S△AOB |
| S△BOC |
∴
| AE |
| BE |
| AF |
| CF |
∴EF∥BC．
点评：本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例；如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边．
练习册系列答案
天天练口算系列答案
相关题目
如图，已知第一象限内的点A在反比例函数y=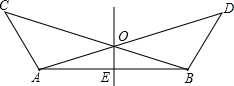
如图所示，∠BAC=∠ABD，AC=BD，点O是AD、BC的交点，点E是AB的中点．
如图所示，⊙O1与⊙O2外切于点P，并且⊙O与⊙O1、⊙O2分别内切于M、N，△O1O2O的周长为36cm，求⊙O的半径长．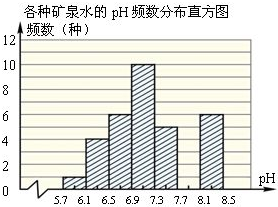
2008年 5月12日，我国四川省发生里氏8.0级地震，社会各界纷纷伸出援助之手捐钱捐物．根据国家质检总局的通知要求，对送往灾区食品、重要消费品必须进行检验检测，以确保运往灾区的食品等救灾物资的质量安全．如图是对某批数种矿泉水的抽查统计图，请观察图形，并回答下列问题：