题目内容
画出函数y=2x+1的图象,利用图象求:
(1)方程2x+1=0的根;
(2)不等式2x+1≥0的解集;
(3)当y≤3时,求x的取值范围;
(4)当-3≤y≤3时,求x的取值范围;
(5)求直线和坐标轴围成的三角形的面积.
(1)方程2x+1=0的根;
(2)不等式2x+1≥0的解集;
(3)当y≤3时,求x的取值范围;
(4)当-3≤y≤3时,求x的取值范围;
(5)求直线和坐标轴围成的三角形的面积.
考点:一次函数与一元一次不等式,一次函数的图象,一次函数与一元一次方程
专题:数形结合
分析:(1)观察函数图象,找出直线y=2x+1与x轴的交点的横坐标即可;
(2)观察函数图象,易得当x≥-
时,y≥0;
(3)观察函数图象,易得当x≤1时,y≤3
(4)利用函数图象得到当x=1时,y=3;当x=-2时,y=-3,则当-3≤y≤3时,-2≤x≤1;
(5)根据三角形面积公式求解.
(2)观察函数图象,易得当x≥-
| 1 |
| 2 |
(3)观察函数图象,易得当x≤1时,y≤3
(4)利用函数图象得到当x=1时,y=3;当x=-2时,y=-3,则当-3≤y≤3时,-2≤x≤1;
(5)根据三角形面积公式求解.
解答:解: (1)如图,当x=-
(1)如图,当x=-
时,y=0,
所以方程2x+1=0的根为x=-
;
(2)当x≥-
时,y≥0,
所以不等式2x+1≥0的解集为x≥-
;
(3)当x=1时,y=3,
所以当x≤1时,y≤3;
(4)当-3≤y≤3时,-2≤x≤1;
(5)直线和坐标轴围成的三角形的面积=
•
•1=
.
 (1)如图,当x=-
(1)如图,当x=-| 1 |
| 2 |
所以方程2x+1=0的根为x=-
| 1 |
| 2 |
(2)当x≥-
| 1 |
| 2 |
所以不等式2x+1≥0的解集为x≥-
| 1 |
| 2 |
(3)当x=1时,y=3,
所以当x≤1时,y≤3;
(4)当-3≤y≤3时,-2≤x≤1;
(5)直线和坐标轴围成的三角形的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
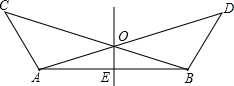 如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.
如图所示,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.
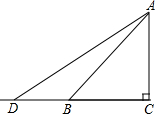 如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为15m,它的坡角为45°,为了提高该堤的防洪能力,现将背水坡改造成坡度为1:1.6的斜坡AD.在CB方向距B处5m处有一座房屋,问在背水坡改造的施工过程中,此处房屋是否需要拆除?
如图,Rt△ABC是一防洪堤背水坡的横截面图,斜坡AB的长为15m,它的坡角为45°,为了提高该堤的防洪能力,现将背水坡改造成坡度为1:1.6的斜坡AD.在CB方向距B处5m处有一座房屋,问在背水坡改造的施工过程中,此处房屋是否需要拆除?