题目内容
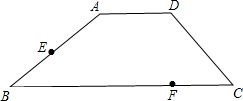 如图,在梯形ABCD中,AD∥BC,AD=DC=4,BC=8.点F在BC上CF=2,E是AB中点.
如图,在梯形ABCD中,AD∥BC,AD=DC=4,BC=8.点F在BC上CF=2,E是AB中点.(1)求证:AC平分∠BCD;
(2)在AC上找一点M,使EM+FM的值最小,请你说明最小的理由,并求出这个最小值.
考点:梯形,全等三角形的判定与性质,轴对称-最短路线问题
专题:
分析:(1)若要证明ACAC平分∠BCD,只要证明∠BCA=∠DCA即可;
(2)过点F作FG⊥AC于G,并延长交CD于N,连接EN交AC于M,连接MF,易证EN为梯形的中位线,求得EN即可.
(2)过点F作FG⊥AC于G,并延长交CD于N,连接EN交AC于M,连接MF,易证EN为梯形的中位线,求得EN即可.
解答:(1)证明:∵AD=DC,
∴∠DAC=∠DCA.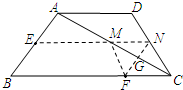
∵AD∥BC,
∴∠DAC=∠BCA.
∴∠BCA=∠DCA.
即AC平分∠BCD.
(2)解:过点F作FG⊥AC于G,并延长交CD于N,连接EN交AC于M,连接MF.
∵∠BCA=∠DCA,∠FGC=∠NGC,GC=GC,
∴△CFG≌△CNG.
∴CF=CN=2.
∴GF=GN,
∴FM=MN,
∵E,M,N在一条直线上,
∴EM+MN最短,
∴EM+FM最短.
∵CD=4,
∴CN=DN=2.
∵E是AB中点,
∴EN=
(AD+BC)=
(4+8)=6,
∴EM+FM=EM+MN=EN=6.
∴∠DAC=∠DCA.

∵AD∥BC,
∴∠DAC=∠BCA.
∴∠BCA=∠DCA.
即AC平分∠BCD.
(2)解:过点F作FG⊥AC于G,并延长交CD于N,连接EN交AC于M,连接MF.
∵∠BCA=∠DCA,∠FGC=∠NGC,GC=GC,
∴△CFG≌△CNG.
∴CF=CN=2.
∴GF=GN,
∴FM=MN,
∵E,M,N在一条直线上,
∴EM+MN最短,
∴EM+FM最短.
∵CD=4,
∴CN=DN=2.
∵E是AB中点,
∴EN=
| 1 |
| 2 |
| 1 |
| 2 |
∴EM+FM=EM+MN=EN=6.
点评:本题主要考查了梯形的性质的应用、最短路线问题,在直线L上的同侧有两个点A、B,在直线L上有到A、B的距离之和最短的点存在,可以通过轴对称来确定,即作出其中一点关于直线L的对称点,对称点与另一点的连线与直线L的交点就是所要找的点.

练习册系列答案
相关题目
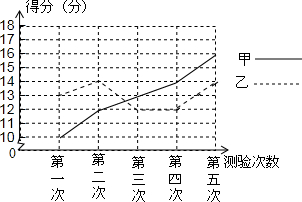 甲乙两人参加某体育项目训练,近期的五次测验得分情况(单位:分)如图所示
甲乙两人参加某体育项目训练,近期的五次测验得分情况(单位:分)如图所示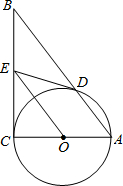 如图在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.
如图在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.
 如图,点B、F、C、D在同一直线上,点A和点E分别在直线BD的两侧,且AB=ED,AC=EF,BF=DC,求证:AB∥DE.
如图,点B、F、C、D在同一直线上,点A和点E分别在直线BD的两侧,且AB=ED,AC=EF,BF=DC,求证:AB∥DE. 如图所示的网络图中,每个小正方形的边长为1,△ABC的三个顶点都在格点上,把△ABC绕着A点逆时针旋转90°后得到△AB′C′.
如图所示的网络图中,每个小正方形的边长为1,△ABC的三个顶点都在格点上,把△ABC绕着A点逆时针旋转90°后得到△AB′C′.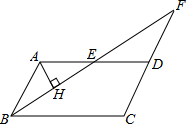 如图,?ABCD中,BC=6,∠ABC的平分线与CD的延长线相交于点F,与AD交于点E,且点E为AD边的中点,过点A作BF的垂线,垂足为H.若AH=2,则BF的长为
如图,?ABCD中,BC=6,∠ABC的平分线与CD的延长线相交于点F,与AD交于点E,且点E为AD边的中点,过点A作BF的垂线,垂足为H.若AH=2,则BF的长为