题目内容
 如图,点B、F、C、D在同一直线上,点A和点E分别在直线BD的两侧,且AB=ED,AC=EF,BF=DC,求证:AB∥DE.
如图,点B、F、C、D在同一直线上,点A和点E分别在直线BD的两侧,且AB=ED,AC=EF,BF=DC,求证:AB∥DE.考点:全等三角形的判定与性质,平行线的判定
专题:证明题
分析:根据题目条件证明△ACB≌△DFE,然后利用全等三角形的性质可以证明题目结论.
解答:证明:∵BF=DC,
∴BF+FC=DC+FC,
∴BC=DF,
在△ACB≌△DFE中,
,
∴△ACB≌△DFE(SSS),
∴∠B=∠D,
∴AB∥DE.
∴BF+FC=DC+FC,
∴BC=DF,
在△ACB≌△DFE中,
|
∴△ACB≌△DFE(SSS),
∴∠B=∠D,
∴AB∥DE.
点评:本题考查了全等三角形的判定方法;此题比较简单,主要利用全等三角形的性质与判定解决题目问题.

练习册系列答案
相关题目
 如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,请画出平移后的图形,并写出△A′B′C′各顶点的坐标.
如图,将△ABC向右平移5个单位长度,再向下平移2个单位长度,得到△A′B′C′,请画出平移后的图形,并写出△A′B′C′各顶点的坐标.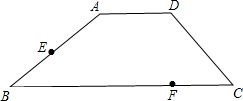 如图,在梯形ABCD中,AD∥BC,AD=DC=4,BC=8.点F在BC上CF=2,E是AB中点.
如图,在梯形ABCD中,AD∥BC,AD=DC=4,BC=8.点F在BC上CF=2,E是AB中点. 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
 如图,已知双曲线y=
如图,已知双曲线y= 如图,是象棋棋盘的一部分.若
如图,是象棋棋盘的一部分.若 位于点(1,-2)上,
位于点(1,-2)上, 位于点(3,-2)上,则
位于点(3,-2)上,则 位于点
位于点