题目内容
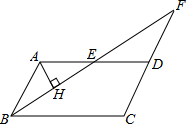 如图,?ABCD中,BC=6,∠ABC的平分线与CD的延长线相交于点F,与AD交于点E,且点E为AD边的中点,过点A作BF的垂线,垂足为H.若AH=2,则BF的长为
如图,?ABCD中,BC=6,∠ABC的平分线与CD的延长线相交于点F,与AD交于点E,且点E为AD边的中点,过点A作BF的垂线,垂足为H.若AH=2,则BF的长为考点:平行四边形的性质,勾股定理
专题:
分析:根据平行四边形的性质和角平分线的定义可求出AB=AE,再根据等腰三角形的性质可求出BH的长,进而可求出BE的长,易证△ABE≌△FDE,所以BE=EF,所以BF=2BE,问题得解.
解答:解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC=6,
∵∠AEB=∠EBC,
∵∠ABC的平分线与CD的延长线相交于点F,
∴∠ABE=∠EBC,
∴∠AEB=∠ABE,
∴AB=AE,
∵点E为AD边的中点,过点A作BF的垂线,垂足为H.
∴BH=
=
,
∴BE=2
,
易证△ABE≌△FDE,
∴BF=2BE=4
,
故答案为:4
.

∴AD∥BC,AD=BC=6,
∵∠AEB=∠EBC,
∵∠ABC的平分线与CD的延长线相交于点F,
∴∠ABE=∠EBC,
∴∠AEB=∠ABE,
∴AB=AE,
∵点E为AD边的中点,过点A作BF的垂线,垂足为H.
∴BH=
| AB2-AH2 |
| 5 |
∴BE=2
| 5 |
易证△ABE≌△FDE,
∴BF=2BE=4
| 5 |
故答案为:4
| 5 |
点评:本题考查了平行四边形的性质、角平分线的定义、等腰三角形的判定和性质、勾股定理的运用,题目的综合性较强,难度中等.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
顺次连结正方形各边中点所成的四边形的面积与原正方形的面积之比为( )
A、1:
| ||
B、1:
| ||
| C、1:3 | ||
| D、1:2 |
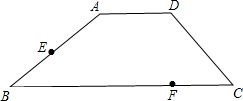 如图,在梯形ABCD中,AD∥BC,AD=DC=4,BC=8.点F在BC上CF=2,E是AB中点.
如图,在梯形ABCD中,AD∥BC,AD=DC=4,BC=8.点F在BC上CF=2,E是AB中点. 如图,在平行四边形ABCD中,E,F分别是对角线BD上的两点,且BE=DF.求证:AE=CF.
如图,在平行四边形ABCD中,E,F分别是对角线BD上的两点,且BE=DF.求证:AE=CF. 如图,直线l与直线AB、CD分别相交于E、F,∠1=105°,当∠2=
如图,直线l与直线AB、CD分别相交于E、F,∠1=105°,当∠2= 如图,是象棋棋盘的一部分.若
如图,是象棋棋盘的一部分.若 位于点(1,-2)上,
位于点(1,-2)上, 位于点(3,-2)上,则
位于点(3,-2)上,则 位于点
位于点