题目内容
1．（1）解方程：3x2-5x+2=0（2）计算：2cos245°-cos230°-tan45°．
分析 （1）把方程左边化为两个因式积的形式，进而可得出结论；
（2）分别把各特殊角的三角函数值代入进行计算即可．
解答 解：（1）原方程可化为（3x+1）（x-2）=0，
故3x+1=0或x-2=0，解得x1=-$\frac{1}{3}$，x2=2；
（2）原式=2×（$\frac{\sqrt{2}}{2}$）2-（$\frac{\sqrt{3}}{2}$）2-1
=2×$\frac{1}{2}$-$\frac{3}{4}$-1
=1-$\frac{3}{4}$-1
=-$\frac{3}{4}$．
点评 本题考查的是因式分解法解一元二次方程，因式分解法就是利用因式分解求出方程的解的方法，这种方法简便易用，是解一元二次方程最常用的方法．
练习册系列答案
相关题目
11．
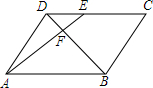如图，在?ABCD中，点E在CD上，连接AE、BD，且AE、BD交于点F，若EC：DE=4：3，则△DEF与△BAF的周长比是（ ）
如图，在?ABCD中，点E在CD上，连接AE、BD，且AE、BD交于点F，若EC：DE=4：3，则△DEF与△BAF的周长比是（ ）| A． | $\frac{4}{3}$ | B． | $\frac{16}{9}$ | C． | $\frac{3}{7}$ | D． | $\frac{7}{3}$ |
12．下列等式正确的是（ ）
| A． | （-1）0=-1 | B． | （-1）-1=1 | C． | 2x-2=$\frac{1}{{2{x^2}}}$ | D． | x-2y2=$\frac{y^2}{x^2}$ |
9．由二次函数y=2x2的图象先向上、再向右各平移2个单位长度得（ ）
| A． | y=2（x-2）2+2 | B． | y=2（x+2）2-2 | C． | y=2（x-2）2-2 | D． | y=2（x+2）2+2 |
作图题：（要求保留作图痕迹，不写作法）