题目内容
16.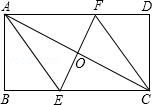 将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,
将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,(1)求证:四边形AECF为菱形;
(2)若AB=12,BC=18,求菱形AECF的边长.
分析 (1)根据折叠的性质得OA=OC,EF⊥AC,EA=EC,再利用AD∥AC得到∠FAC=∠ECA,则可根据“ASA”判断△AOF≌△COE,得到OF=OE,加上OA=OC,AC⊥EF,于是可根据菱形的判定方法得到四边形AECF为菱形;
(2)设菱形的边长为x,则BE=BC-CE=8-x,AE=x,在Rt△ABE中根据勾股定理得(8-x)2+42=x2,然后解方程即可得到菱形的边长.
解答 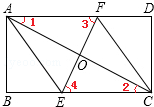 (1)证明:∵矩形ABCD折叠使A,C重合,折痕为EF,
(1)证明:∵矩形ABCD折叠使A,C重合,折痕为EF,
∴OA=OC,EF⊥AC,EA=EC,
∵AD∥AC,
∴∠FAC=∠ECA,
在△AOF和△COE中,$\left\{\begin{array}{l}{∠FAO=∠ECO}&{\;}\\{AO=CO}&{\;}\\{∠AOF=∠COE}&{\;}\end{array}\right.$,
∴△AOF≌△COE(ASA),
∴OF=OE,
∵OA=OC,
∴四边形AECF时平行四边形,
又∵AC⊥EF,
∴四边形AECF为菱形;
(2)解:设菱形的边长为x,则BE=BC-CE=18-x,AE=x,
在Rt△ABE中,∵BE2+AB2=AE2,
∴(18-x)2+122=x2,
解得:x=13,
即菱形的边长为13.
点评 本题考查了菱形的判定与性质、矩形的性质、全等三角形的判定与性质、菱形的判定与性质、勾股定理;熟练掌握矩形的性质,证明四边形是菱形是解决问题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
7.下列说法正确的有( )个
①连接两点的线段的长叫两点之间的距离;
②直线比线段长;
③若AM=BM,则M为AB的中点;
④由不在同一直线上的几条线段首尾顺次相连所组成的封闭图形叫多边形.
①连接两点的线段的长叫两点之间的距离;
②直线比线段长;
③若AM=BM,则M为AB的中点;
④由不在同一直线上的几条线段首尾顺次相连所组成的封闭图形叫多边形.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
11.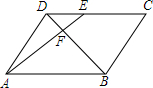 如图,在?ABCD中,点E在CD上,连接AE、BD,且AE、BD交于点F,若EC:DE=4:3,则△DEF与△BAF的周长比是( )
如图,在?ABCD中,点E在CD上,连接AE、BD,且AE、BD交于点F,若EC:DE=4:3,则△DEF与△BAF的周长比是( )
 如图,在?ABCD中,点E在CD上,连接AE、BD,且AE、BD交于点F,若EC:DE=4:3,则△DEF与△BAF的周长比是( )
如图,在?ABCD中,点E在CD上,连接AE、BD,且AE、BD交于点F,若EC:DE=4:3,则△DEF与△BAF的周长比是( )| A. | $\frac{4}{3}$ | B. | $\frac{16}{9}$ | C. | $\frac{3}{7}$ | D. | $\frac{7}{3}$ |
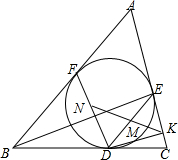 设△ABC的内切圆与BC、CA、AB分别切于D、E、F,M、N分别为DE、DF的中点,直线MN与CA交于K.求证:DK∥BE.
设△ABC的内切圆与BC、CA、AB分别切于D、E、F,M、N分别为DE、DF的中点,直线MN与CA交于K.求证:DK∥BE.



 作图题:(要求保留作图痕迹,不写作法)
作图题:(要求保留作图痕迹,不写作法)