题目内容
14.按要求做题:(1)(1+$\frac{4}{{a}^{2}-4}$)•$\frac{a+2}{a}$.
(2)因式分解:(3x+y)2-(x-3y)2.
分析 (1)先计算括号内分式的加法、并将分母因式分解,再计算乘法即可得;
(2)先利用平方差公式分解,再提取公因式可得.
解答 解:(1)原式=$\frac{{a}^{2}}{(a+2)(a-2)}$•$\frac{a+2}{a}$=$\frac{a}{a-2}$;
(2)原式=[(3x+y)+(x-3y)][(3x+y)-(x-3y)]
=(4x-2y)(2x+4y)
=4(2x-y)(x+2y).
点评 本题主要考查分式的混合运算和因式分解,熟练掌握分式的混合运算步骤及法则、因式分解的基本步骤和平方差公式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.为积极响应北京市创建“全国卫生城市”的号召,某校1 500名学生参加了卫生知识竞赛,成绩记为A、B、C、D四等.从中随机抽取了部分学生成绩进行统计,绘制成如下两幅不完整的统计图表,根据图表信息,以下说法不正确的是( )
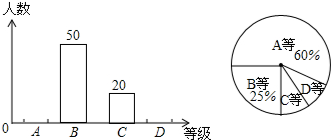

| A. | 样本容量是200 | |
| B. | 样本中C等所占百分比是10% | |
| C. | D等所在扇形的圆心角为15° | |
| D. | 估计全校学生成绩为A等大约有900人 |
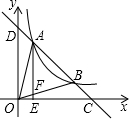 如图,一次函数y=-x+b与反比例函数y=$\frac{4}{x}$(x>0)的图象交于A,B两点,与x轴,y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.
如图,一次函数y=-x+b与反比例函数y=$\frac{4}{x}$(x>0)的图象交于A,B两点,与x轴,y轴分别交于C,D两点,连结OA,OB,过A作AE⊥x轴于点E,交OB于点F,设点A的横坐标为m.