题目内容
4.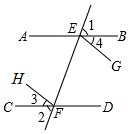 已知,如图,∠1=∠2,∠3=∠4,试说明EG∥FH的道理,以下是说明道理的过程,请将其填写完整,并在括号内填出所得结论的理由.
已知,如图,∠1=∠2,∠3=∠4,试说明EG∥FH的道理,以下是说明道理的过程,请将其填写完整,并在括号内填出所得结论的理由.∵∠1=∠2(已知),
∠AEF=∠1对顶角相等,
∴∠AEF=∠2 (等量代换),
∴AB∥CD同位角相等,两直线平行,
∴∠BEF=∠CEF两直线平行,内错角相等,
∵∠3=∠4(已知)
∴∠BEF-∠4=∠CEF-∠3 (等式的基本性质),
即∠GEF=∠HFE
∴EG∥FH内错角相等,两直线平行.
分析 利用对顶角相等得出∠AEF=∠1,再利用平行线的判定定理和性质定理可得∠BEF=∠CEF,易得∠GEF=∠HFE,利用内错角相等,两直线平行可得结论.
解答 解:∵∠1=∠2(已知),
∠AEF=∠1 (对顶角相等),
∴∠AEF=∠2 (等量代换),
∴AB∥CD (同位角相等,两直线平行),
∴∠BEF=∠CEF (两直线平行,内错角相等),
∵∠3=∠4(已知)
∴∠BEF-∠4=∠CEF-∠3 (等式的基本性质),
即∴∠GEF=∠HFE
∴EG∥FH (内错角相等,两直线平行).
故答案为:对顶角相等;同位角相等,两直线平行;两直线平行,内错角相等;GEF;内错角相等,两直线平行.
点评 本题考查的是平行线的判定与性质,熟知平行线的判定定理是解答此题的关键.

练习册系列答案
相关题目
12.已知am=2,an=3,ap=4,则a2m+3n-p的值为( )
| A. | 36 | B. | 27 | C. | 9 | D. | 6 |
12.关于x的方程ax2-2x+1=0有两个实数根,则a的取值范围是( )
| A. | .a≤1 | B. | .a<1 | C. | .a≤1且a≠0 | D. | a<1且a≠0 |
14.下列各数中,无理数是( )
| A. | $\sqrt{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{22}{7}$ | D. | 0.16 |

 已知一次函数y=kx+b的图象经过点A(-3,0),B(2,5)两点.正比例函数y=kx的图象经过点B(2,3).
已知一次函数y=kx+b的图象经过点A(-3,0),B(2,5)两点.正比例函数y=kx的图象经过点B(2,3).