题目内容
12.关于x的方程ax2-2x+1=0有两个实数根,则a的取值范围是( )| A. | .a≤1 | B. | .a<1 | C. | .a≤1且a≠0 | D. | a<1且a≠0 |
分析 若a=0,方程化为一元一次方程,只有一个解,不合题意;故a不为0,方程即为一元二次方程,根据方程有两个实数根,得到根的判别式大于等于0,列出关于a的不等式,求出不等式的解集,即可得到a的范围.
解答 解:ax2-2x+1=0有两个实数根,
当a=0时,方程化为-2x+1=0,解得:x=$\frac{1}{2}$,不合题意;
故a≠0,则有b2-4ac=4-4a≥0,
解得:a≤1,
则m的取值范围是a≤1且a≠0.
故选C.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20. 如图,下面几何体的俯视图是( )
如图,下面几何体的俯视图是( )
 如图,下面几何体的俯视图是( )
如图,下面几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
1.|-3|结果为( )
| A. | -3 | B. | 3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
18.已知m,n是关于x的一元二次方程x2-2tx+t2-2t+4=0的两实数根,则(m+2)(n+2)的最小值是( )
| A. | 7 | B. | 11 | C. | 12 | D. | 16 |
17. 如图,在△ABC中,AB=AC,且D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,则∠AFD的度数是( )
如图,在△ABC中,AB=AC,且D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,则∠AFD的度数是( )
 如图,在△ABC中,AB=AC,且D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,则∠AFD的度数是( )
如图,在△ABC中,AB=AC,且D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,则∠AFD的度数是( )| A. | 160° | B. | 150° | C. | 140° | D. | 120° |
1.二次根式$\sqrt{2-a}$有意义,a的范围是( )
| A. | a>-2 | B. | a<-2 | C. | a=±2 | D. | a≤2 |
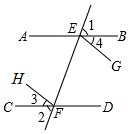 已知,如图,∠1=∠2,∠3=∠4,试说明EG∥FH的道理,以下是说明道理的过程,请将其填写完整,并在括号内填出所得结论的理由.
已知,如图,∠1=∠2,∠3=∠4,试说明EG∥FH的道理,以下是说明道理的过程,请将其填写完整,并在括号内填出所得结论的理由. 如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.
如图,在四边形ABCD中,点H是BC的中点,作射线AH,在线段AH及其延长线上分别取点E,F,连结BE,CF.