题目内容
9.若函数y=(m-2)x|m|-3是反比例函数,则m=-2;使分式$\frac{{\sqrt{x+2}}}{x}$有意义的x的取值范围是x≥-2且x≠0.分析 由反比例函数的定义得到|m|-3=-1且m-2≠0,由此求得m的值.
根据二次根式的性质和分式的意义,被开方数大于等于0,分母不等于0,就可以求解.
解答 解:依题意得:|m|-3=-1且m-2≠0,
解得m=-2.
根据题意得:x+2≥0且x≠0,
解得:x≥-2且x≠0.
故答案为:-2;x≥-2且x≠0.
点评 本题考查了反比例函数的定义,反比例函数的一般形式是$y=\frac{k}{x}$(k≠0)或y=kx-1.同时考查了分式、二次根式有意义的条件:分式有意义,分母不为0;二次根式的被开方数是非负数.应注意在求得取值后应排除不在取值范围内的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知m,n是关于x的一元二次方程x2-2tx+t2-2t+4=0的两实数根,则(m+2)(n+2)的最小值是( )
| A. | 7 | B. | 11 | C. | 12 | D. | 16 |
17.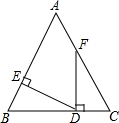 如图,在△ABC中,AB=AC,且D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,则∠AFD的度数是( )
如图,在△ABC中,AB=AC,且D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,则∠AFD的度数是( )
 如图,在△ABC中,AB=AC,且D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,则∠AFD的度数是( )
如图,在△ABC中,AB=AC,且D在BC上,DE⊥AB于E,DF⊥BC交AC于点F,若∠EDF=70°,则∠AFD的度数是( )| A. | 160° | B. | 150° | C. | 140° | D. | 120° |
1.二次根式$\sqrt{2-a}$有意义,a的范围是( )
| A. | a>-2 | B. | a<-2 | C. | a=±2 | D. | a≤2 |
19.体育委员统计了全班同学60秒跳绳的次数,并列出不完全的频数分布表:
(1)补全表中信息
(2)跳绳次数在120≤x<210范围的学生占全班学生的百分比是多少?
(3)画出适当的统计图表示上面的信息
(1)补全表中信息
(2)跳绳次数在120≤x<210范围的学生占全班学生的百分比是多少?
(3)画出适当的统计图表示上面的信息
| 次数分组 | 频数 | 频率 |
| 60≤x<90 | 15 | 0.25 |
| 90≤x<120 | 24 | 0.4 |
| 120≤x<150 | 12 | 0.2 |
| 150≤x<180 | 6 | 0.1 |
| 180≤x<210 | 3 | 0.05 |
| 合计 | 60 | 1.00 |

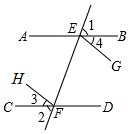 已知,如图,∠1=∠2,∠3=∠4,试说明EG∥FH的道理,以下是说明道理的过程,请将其填写完整,并在括号内填出所得结论的理由.
已知,如图,∠1=∠2,∠3=∠4,试说明EG∥FH的道理,以下是说明道理的过程,请将其填写完整,并在括号内填出所得结论的理由.