题目内容
如果（x+1）（x2-2ax+a2）的乘积中不含x2项，则a= ．
考点：多项式乘多项式
专题：
分析：先利用多项式乘法的运算法则展开求它们的积，并且把a看作常数合并关于x2的同类项，令x2的系数为0，求出a的值．
解答：
解：原式=x3-2ax2+a2x+x2-2ax+a2
=x3+（1-2a）x2+（a2-2a）x+a2，
∵不含x2项，
∴1-2a=0，
解得a=
，
故答案为：
．
=x3+（1-2a）x2+（a2-2a）x+a2，
∵不含x2项，
∴1-2a=0，
解得a=
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查了多项式乘多项式法则，理解不含某一项，就是让这一项的系数等于0是关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
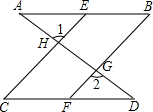如图，直线AD与AB，CD分别相交于点A，D，与EC，BF分别相交于点H，G，如果∠1=∠2，∠B=∠C，试说明∠A=∠D，并写出每一步推理的依据．
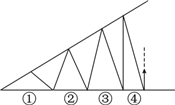如图，不断地将楔形木片分成面积相等的三角形．这时，任意地确定左端最初的三角形后，后面的尺寸自然地就确定了．设下侧的边为①、②、③，等等，问：
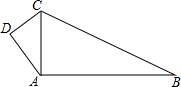如图，∠ADC=90°，AB=24，BC=26，DC=6，AD=8，
如图所示，BC平分∠ABO交y轴正半轴于C点，AB=m，S△ABC=m．则点C的坐标为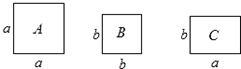
现有若干张卡片，分别是正方形卡片A、B和长方形卡片C，卡片大小如图所示．如果要拼一个长为（a+2b），宽为（a+b）的大长方形，则需要C类卡片张数为（ ）