题目内容
 如图所示,BC平分∠ABO交y轴正半轴于C点,AB=m,S△ABC=m.则点C的坐标为
如图所示,BC平分∠ABO交y轴正半轴于C点,AB=m,S△ABC=m.则点C的坐标为考点:角平分线的性质,坐标与图形性质
专题:
分析:过点C作CD⊥AB与D,根据三角形的面积求出CD,再根据角平分线上的点到角的两边距离相等可得OC=CD,然后写出点C的坐标即可.
解答:
 解:如图,过点C作CD⊥AB与D,
解:如图,过点C作CD⊥AB与D,
∵AB=m,S△ABC=m,
∴CD=2,
∵BC是∠ABO的平分线,
∴OC=CD=2,
∴点C的坐标为(0,2).
故答案为:(0,2).
 解:如图,过点C作CD⊥AB与D,
解:如图,过点C作CD⊥AB与D,∵AB=m,S△ABC=m,
∴CD=2,
∵BC是∠ABO的平分线,
∴OC=CD=2,
∴点C的坐标为(0,2).
故答案为:(0,2).
点评:本题考查了角平分线上的点到角的两边距离相等的性质,坐标与图形性质,熟记性质并作辅助线构造出与OC相等的线段是解题的关键.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
下列计算正确的是( )
| A、a2+a3=a5 |
| B、a•a2=a2 |
| C、(ab)3=ab3 |
| D、(-a2)2=a4 |
下列说法正确的是( )
| A、有理数是有限小数 |
| B、无限小数是无理数 |
| C、数轴上的点与实数一一对应 |
| D、实数分为正实数和负实数 |
图字母所代表的正方形的面积为144的选项为( )
A、 |
B、 |
C、 |
D、 |
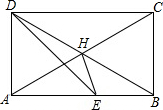 如图,在矩形ABCD中,对角线DB=2AD,DE平分∠CDA,求∠HED的度数.
如图,在矩形ABCD中,对角线DB=2AD,DE平分∠CDA,求∠HED的度数.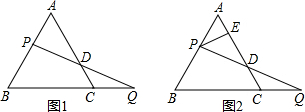
 如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有( )
如图,在正方形方格中,阴影部分是涂黑7个小正方形所形成的图案,再将方格内空白的一个小正方形涂黑,使得到的新图案成为一个轴对称图形的涂法有( )