Question

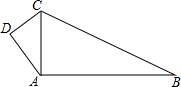如图，∠ADC=90°，AB=24，BC=26，DC=6，AD=8，
（1）求AC的长；
（2）求四边形ABCD的面积．

Answer 1

考点：勾股定理,勾股定理的逆定理

专题：计算题

分析：（1）在直角三角形ACD中，由DC与AD的长，利用勾股定理求出AC的长即可；
（2）由AC，AB以及BC的长，利用勾股定理的逆定理得到三角形ABC为直角三角形，四边形ABCD面积=直角三角形ACD面积+直角三角形ABC面积，求出即可．

解答： 解：（1）在Rt△ACD中，DC=6，AD=8，
根据勾股定理得：AC=

AD2+CD2

=10；
（2）∵AC=10，AB=24，BC=26，
∴AC²+AB²=676，BC²=676，即AC²+AB²=BC²，
∴△ABC为直角三角形，
则S_{四边形ABCD}=S_△ACD+S_△ABC=

1

2

×6×8+

1

2

×10×24=24+120=144．

点评：此题考查了勾股定理，以及勾股定理的逆定理，熟练掌握勾股定理是解本题的关键．