题目内容
19. 如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,DE⊥BD,D,E分别为垂足,F为AB的中点,若以点D为圆心,$\frac{1}{2}$CD为半径画⊙D,试判定B,E,F与⊙D的位置关系.
如图,在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,DE⊥BD,D,E分别为垂足,F为AB的中点,若以点D为圆心,$\frac{1}{2}$CD为半径画⊙D,试判定B,E,F与⊙D的位置关系.
分析 设AB=2x,再由在Rt△ABC中,∠ACB=90°,∠A=30°,CD⊥AB,DE⊥BD,可用x表示出DF,BD即DE,CD的长,再与$\frac{1}{2}$CD相比较即可.
解答 解:设AB=2x,
∵∠ACB=90°,∠A=30°,F为AB的中点,
∴BC=x,BF=x,AC=$\sqrt{3}$x,
∵CD⊥AB,
∴CD=$\frac{AC•BC}{AB}$=$\frac{\sqrt{3}x•x}{2x}$=$\frac{\sqrt{3}x}{2}$,
∴⊙D的半径为$\frac{\sqrt{3}x}{4}$.
∵∠ACB=90°,∠A=30°,CD⊥AB,
∴∠B=60°,
∴BD=$\frac{1}{2}$BC=$\frac{x}{2}$>$\frac{\sqrt{3}x}{4}$,
∴点B在圆外;
∵DE=$\frac{CD•BD}{BC}$=$\frac{\frac{\sqrt{3}}{2}x•\frac{x}{2}}{x}$=$\frac{\sqrt{3}x}{4}$=⊙D的半径,
∴点E在圆上;
∵DF=$\frac{1}{2}$AB-BD=x-$\frac{x}{2}$=$\frac{x}{2}$>$\frac{\sqrt{3}x}{4}$,
∴点F在圆外.
点评 本题考查的是点与圆的位置关系,熟知点与圆的三种位置关系是解答此题的关键.

练习册系列答案
相关题目
 在长为10m,宽为8m的矩形空地上,沿平行于矩形各边的方向分割出三个全等的小矩形花圃,要使小矩形花圃的面积和为24m2,示意图如图所示,求其中一个小矩形花圃的长和宽.
在长为10m,宽为8m的矩形空地上,沿平行于矩形各边的方向分割出三个全等的小矩形花圃,要使小矩形花圃的面积和为24m2,示意图如图所示,求其中一个小矩形花圃的长和宽.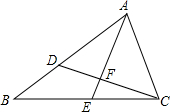 如图,已知AD=2,DB=1,∠ACD=∠B,∠BAC的平分线分别交CD,BC于F,求$\frac{AF}{AE}$的值.
如图,已知AD=2,DB=1,∠ACD=∠B,∠BAC的平分线分别交CD,BC于F,求$\frac{AF}{AE}$的值.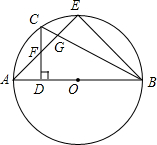 如图,AB是⊙O的直径,AE是弦,CF=GF,CD⊥AB于D,交AE于F,CB交AE于G.求证:C是$\widehat{AE}$的中点.
如图,AB是⊙O的直径,AE是弦,CF=GF,CD⊥AB于D,交AE于F,CB交AE于G.求证:C是$\widehat{AE}$的中点. 如图所示的抛物线的解析式为y=2x2-4x+2.
如图所示的抛物线的解析式为y=2x2-4x+2.