题目内容
17.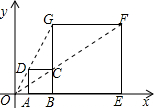 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )| A. | (3,2) | B. | (3,1) | C. | (2,2) | D. | (4,2) |
分析 直接利用位似图形的性质结合相似比得出AD的长,进而得出△OAD∽△OBG,进而得出AO的长,即可得出答案.
解答 解:∵正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,
∴$\frac{AD}{BG}$=$\frac{1}{3}$,
∵BG=6,
∴AD=BC=2,
∵AD∥BG,
∴△OAD∽△OBG,
∴$\frac{OA}{OB}$=$\frac{1}{3}$,
∴$\frac{OA}{2+OA}$=$\frac{1}{3}$,
解得:OA=1,
∴OB=3,
∴C点坐标为:(3,2),
故选:A.
点评 此题主要考查了位似变换以及相似三角形的判定与性质,正确得出AO的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.某次列车平均提速20km/h,用相同的时间,列车提速前行驶400km,提速后比提速前多行驶100km,设提速前列车的平均速度为xkm/h,下列方程正确的是( )
| A. | $\frac{400}{x}$=$\frac{400+100}{x+20}$ | B. | $\frac{400}{x}$=$\frac{400-100}{x-20}$ | ||
| C. | $\frac{400}{x}$=$\frac{400+100}{x-20}$ | D. | $\frac{400}{x}$=$\frac{400-100}{x+20}$ |
7.不等式组$\left\{\begin{array}{l}x+2>0\\ 2x-1≤0\end{array}\right.$的所有整数解是( )
| A. | -1、0 | B. | -2、-1 | C. | 0、1 | D. | -2、-1、0 |
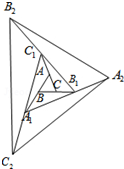 如图,△ABC的面积为1.第一次操:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.
如图,△ABC的面积为1.第一次操:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2016,最少经过( )次操作.
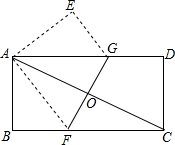 如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB=4,BC=8,则△ABF的面积为6.
如图,将一矩形纸片ABCD折叠,使两个顶点A,C重合,折痕为FG.若AB=4,BC=8,则△ABF的面积为6. 如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为$\frac{1}{4}$πcm2.
如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为$\frac{1}{4}$πcm2. 如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).
如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(-3,5),B(-2,1),C(-1,3).