题目内容

7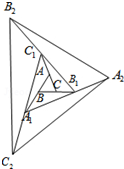．如图，△ABC的面积为1．第一次操：分别延长AB，BC，CA至点A1，B1，C1，使A1B=AB，B1C=BC，C1A=CA，顺次连接A1，B1，C1，得到△A1B1C1．第二次操作：分别延长A1B1，B1C1，C1A1至点A2，B2，C2，使A2B1=A1B1，B2C1=B1C1，C2A1=C1A1，顺次连接A2，B2，C2，得到△A2B2C2，…按此规律，要使得到的三角形的面积超过2016，最少经过（　　）次操作．
A．6B．5C．4D．3

分析 先根据已知条件求出△A1B1C1及△A2B2C2的面积，再根据两三角形的倍数关系求解即可．

解答 解：△ABC与△A1BB1底相等（AB=A1B），高为1：2（BB1=2BC），故面积比为1：2，
∵△ABC面积为1，
∴S△A1BB1=2．
同理可得，S△C1B1C=2，S△AA1C=2，
∴S△A1B1C1=S△C1B1C+S△AA1C+S△A1B1B+S△ABC=2+2+2+1=7；
同理可证S△A2B2C2=7S△A1B1C1=49，
第三次操作后的面积为7×49=343，
第四次操作后的面积为7×343=2401．
故按此规律，要使得到的三角形的面积超过2016，最少经过4次操作，
故选：C．

点评 本题考查了图形的变化规律，解答此题的关键是找出相邻两次操作之间三角形面积的关系，再根据此规律求解即可．

练习册系列答案
相关题目
17．如图，在平面直角坐标系中，已知△AOB是等边三角形，点A的坐标是（0，4），点B在第一象限，点P是x轴上的一个动点，连接AP，并把△AOP绕着点A按逆时针方向旋转，使边AO与AB重合，得到△ABD．
（1）求B的坐标；
（2）当点P运动到点（t，0）时，试用含t的式子表示点D的坐标；
（3）是否存在点P，使△OPD的面积等于$\frac{\sqrt{3}}{4}$，若存在，请求出符合条件的点P的坐标（直接写出结果即可）
18．已知AB是⊙O直径，点C、D是⊙O上两点，连接AD、CD、AC．
（1）如图1，过点D作⊙O的切线MN，当MN∥AC时，求证：∠ADM=∠ADN；
（2）如图2，连接BD交AC于点E，当CD=OA时，求证：∠BEC=60°；
（3）在（2）的条件下，取$\widehat{AB}$中点F，若E为BD中点，CD=7，求EF的长．
15．下列分式中，最简分式是（　　）
A．$\frac{2+a}{{-4-4a-{a^2}}}$B．$\frac{a-b}{b-a}$C．$\frac{{{x^2}-4}}{x-2}$D．$\frac{{{x^2}+{y^2}}}{x+y}$
2．在?ABCD中，点E、F分别在AB、CD上，且AE=CF．求证：DE=BF．
12．已知，在矩形ABCD中，AB=a，BC=b，动点M从点A出发沿边AD向点D运动（点M与点A、点D不重合）．
（1）如图1，当b=2a，点M运动到边AD的中点时，请证明∠BMC=90°；
（2）如图2，当a=2，b=5，求点M运动到什么位置时，∠BMC=90°；
（3）如图3，在第（2）问的条件下，若另一动点N从点C出发沿边C→M→B运动，且点M、点N的出发时间与运动速度都相同，过点N作AD和垂线交AD于点H，当△MNH与△MBC相似时，求MH的长．
19．用直尺和圆规作Rt△ABC斜边AB上的高线CD，以下四个作图中，作法错误的是（　　）
A．B．C．D．
16．如图1，在直角坐标系xoy中，直线l：y=kx+b交x轴，y轴于点E，F，点B的坐标是（2，2），过点B分别作x轴、y轴的垂线，垂足为A、C，点D是线段CO上的动点，以BD为对称轴，作与△BCD成轴对称的△BC′D．
（1）当∠CBD=15°时，求点C′的坐标．
（2）当图1中的直线l经过点A，且k=-$\frac{\sqrt{3}}{3}$时（如图2），求点D由C到O的运动过程中，线段BC′扫过的图形与△OAF重叠部分的面积．
（3）当图1中的直线l经过点D，C′时（如图3），以DE为对称轴，作与△DOE成轴对称的△DO′E，连结O′C，O′O，问是否存在点D，使得△DO′E与△CO′O相似？若存在，求出k、b的值；若不存在，请说明理由．
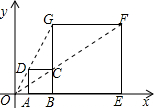17．如图，在平面直角坐标中，正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形，且相似比为$\frac{1}{3}$，点A，B，E在x轴上，若正方形BEFG的边长为6，则C点坐标为（　　）
A．（3，2）B．（3，1）C．（2，2）D．（4，2）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网