题目内容
5.某次列车平均提速20km/h,用相同的时间,列车提速前行驶400km,提速后比提速前多行驶100km,设提速前列车的平均速度为xkm/h,下列方程正确的是( )| A. | $\frac{400}{x}$=$\frac{400+100}{x+20}$ | B. | $\frac{400}{x}$=$\frac{400-100}{x-20}$ | ||
| C. | $\frac{400}{x}$=$\frac{400+100}{x-20}$ | D. | $\frac{400}{x}$=$\frac{400-100}{x+20}$ |
分析 直接利用相同的时间,列车提速前行驶400km,提速后比提速前多行驶100km,进而得出等式求出答案.
解答 解:设提速前列车的平均速度为xkm/h,根据题意可得:
$\frac{400}{x}$=$\frac{400+100}{x+20}$.
故选:A.
点评 此题主要考查了由实际问题抽象出分式方程,根据题意得出正确等量关系是解题关键.

练习册系列答案
相关题目
15.下列分式中,最简分式是( )
| A. | $\frac{2+a}{{-4-4a-{a^2}}}$ | B. | $\frac{a-b}{b-a}$ | C. | $\frac{{{x^2}-4}}{x-2}$ | D. | $\frac{{{x^2}+{y^2}}}{x+y}$ |
17.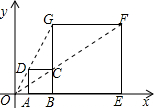 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )| A. | (3,2) | B. | (3,1) | C. | (2,2) | D. | (4,2) |
14. 如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
 如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )| A. | 50° | B. | 60° | C. | 120° | D. | 130° |
15. 实数a,b在数轴上的位置如图所示,则|a|-|b|可化简为( )
实数a,b在数轴上的位置如图所示,则|a|-|b|可化简为( )
 实数a,b在数轴上的位置如图所示,则|a|-|b|可化简为( )
实数a,b在数轴上的位置如图所示,则|a|-|b|可化简为( )| A. | a-b | B. | b-a | C. | a+b | D. | -a-b |
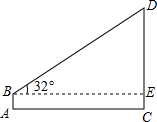 在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)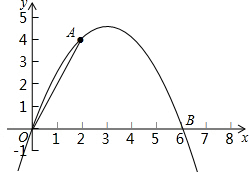 如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).
如图,二次函数y=ax2+bx的图象经过点A(2,4)与B(6,0).