题目内容
2. 如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为$\frac{1}{4}$πcm2.
如图,C为半圆内一点,O为圆心,直径AB长为2cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为$\frac{1}{4}$πcm2.
分析 根据已知条件和旋转的性质得出两个扇形的圆心角的度数,再根据扇形的面积公式进行计算即可得出答案.
解答 解:∵∠BOC=60°,△B′OC′是△BOC绕圆心O逆时针旋转得到的,
∴∠B′OC′=60°,△BCO=△B′C′O,
∴∠B′OC=60°,∠C′B′O=30°,
∴∠B′OB=120°,
∵AB=2cm,
∴OB=1cm,OC′=$\frac{1}{2}$,
∴B′C′=$\frac{\sqrt{3}}{2}$,
∴S扇形B′OB=$\frac{120π×{1}^{2}}{360}$=$\frac{1}{3}$π,
S扇形C′OC=$\frac{120π×\frac{1}{4}}{360}$=$\frac{π}{12}$,
∵
∴阴影部分面积=S扇形B′OB+S△B′C′O-S△BCO-S扇形C′OC=S扇形B′OB-S扇形C′OC=$\frac{1}{3}$π-$\frac{π}{12}$=$\frac{1}{4}$π;
故答案为:$\frac{1}{4}$π.
点评 此题考查了旋转的性质和扇形的面积公式,掌握直角三角形的性质和扇形的面积公式是本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.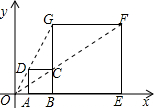 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
 如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为$\frac{1}{3}$,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )| A. | (3,2) | B. | (3,1) | C. | (2,2) | D. | (4,2) |
7.下列计算,正确的是( )
| A. | a2•a2=2a2 | B. | a2+a2=a4 | C. | (-a2)2=a4 | D. | (a+1)2=a2+1 |
14. 如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
 如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )
如图,已知直线a、b被直线c所截.若a∥b,∠1=120°,则∠2的度数为( )| A. | 50° | B. | 60° | C. | 120° | D. | 130° |
11.在线段、平行四边形、矩形、等腰三角形、圆这几个图形中既是轴对称图形又是中心对称图形的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
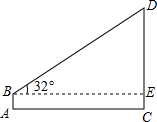 在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
在学习完“利用三角函数测高”这节内容之后,某兴趣小组开展了测量学校旗杆高度的实践活动,如图,在测点A处安置测倾器,量出高度AB=1.5m,测得旗杆顶端D的仰角∠DBE=32°,量出测点A到旗杆底部C的水平距离AC=20m,根据测量数据,求旗杆CD的高度.(参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)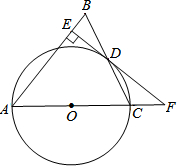 如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.
如图,在△ABC中,AB=AC,以AC边为直径作⊙O交BC边于点D,过点D作DE⊥AB于点E,ED、AC的延长线交于点F.