题目内容
18. 如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连结DF.
如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于点F,连结DF.(1)求证:∠AFD=∠CFE;
(2)若AB∥CD,试说明四边形ABCD是菱形;
(3)在(2)的条件下,试确定E点的位置,使得∠EFD=∠BCD,并说明理由.
分析 (1)先根据SSS证明△ABC≌△ADC得∠BAC=∠DAC,则△ABF≌△ADF,再由对顶角相等可得结论;
(2)根据平行得内错角∠BAC=∠ACD,再由(1)的结论∠BAC=∠DAC,可证得AD=CD,则四边相等,四边形ABCD是菱形;
(3)当EB⊥CD时,∠EFD=∠BCD,理由是:证明△BCF≌△DCF,得∠CBF=∠CDF,则直角△EFD和直角△AEC有两个角对应相等,则∠EFD=∠BCD.
解答 证明:(1)在△ABC和△ADC中,
∵$\left\{\begin{array}{l}{AB=AD}\\{BC=DC}\\{AC=AC}\end{array}\right.$,
∴△ABC≌△ADC(SSS),
∴∠BAC=∠DAC,
又∵AF=AF
∴△ABF≌△ADF,
∴∠AFD=∠AFB,
∵∠AFB=∠CFE,
∴∠AFD=∠CFE;
(2)∵AB∥CD,
∴∠BAC=∠ACD,
又∵∠BAC=∠DAC,
∴∠CAD=∠ACD,
∴AD=CD,
∵AB=AD,CB=CD,
∴AB=CB=CD=AD,
∴四边形ABCD是菱形;
(3)解:当EB⊥CD时,∠EFD=∠BCD,
理由:∵四边形ABCD为菱形,
∴BC=CD,∠BCF=∠DCF,
∴△BCF≌△DCF,
∴∠CBF=∠CDF,
∵BE⊥CD,
∴∠BEC=∠DEF=90°,
∴∠EFD=∠BCD.
点评 本题是四边形的综合题,考查了菱形、全等三角形的性质和判定;菱形常用的判定方法是:四边相等四边形是菱形.

练习册系列答案
相关题目
7. 为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.
为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.
女生进球个数的统计表
(1)求这个班级的男生人数;
(2)补全条形统计图,并计算出扇形统计图中进2个球的扇形的圆心角度数;
(3)该校共有学生1880人,请你估计全校进球数不低于3个的学生大约有1160人.
 为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.
为了解“足球进校园”活动开展情况,某中学利用体育课进行了定点射门测试,每人射门5次,所有班级测试结束后,随机抽取了某班学生的射门情况作为样本,对进球的人数进行整理后,绘制了不完整的统计图表,该班女生有22人,女生进球个数的众数为2,中位数为3.女生进球个数的统计表
| 进球数(个) | 人数 |
| 0 | 1 |
| 1 | 2 |
| 2 | x |
| 3 | y |
| 4 | 4 |
| 5 | 2 |
(2)补全条形统计图,并计算出扇形统计图中进2个球的扇形的圆心角度数;
(3)该校共有学生1880人,请你估计全校进球数不低于3个的学生大约有1160人.
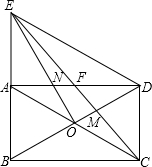 如图,矩形ABCD的对角线交于O点,已知∠ABD=60°,过点O作EO⊥BD交BA延长线于点E,交AD于点N,连接ED、EC,EC分别交AD、BD于点F和点M.
如图,矩形ABCD的对角线交于O点,已知∠ABD=60°,过点O作EO⊥BD交BA延长线于点E,交AD于点N,连接ED、EC,EC分别交AD、BD于点F和点M. 如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,若CD=6,BE=1,则⊙O的直径为10.
如图,AB是⊙O的直径,CD为弦,CD⊥AB于E,若CD=6,BE=1,则⊙O的直径为10. 解不等式组$\left\{\begin{array}{l}{\frac{2x-1}{3}>\frac{1}{2}-\frac{2}{3}①}\\{2x≥3x-1②}\end{array}\right.$请结合填题意空,完成本题的解答
解不等式组$\left\{\begin{array}{l}{\frac{2x-1}{3}>\frac{1}{2}-\frac{2}{3}①}\\{2x≥3x-1②}\end{array}\right.$请结合填题意空,完成本题的解答 由若干个相同的小正方体搭成的一个几何体如图所示,它的俯视图为( )
由若干个相同的小正方体搭成的一个几何体如图所示,它的俯视图为( )



 求证:等腰三角形的两个底角相等
求证:等腰三角形的两个底角相等