题目内容
11.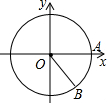 如图,以原点为圆心,2为半径的⊙O与正半轴交于点A,在⊙O上且在x轴的下方有一点B,∠AOB=45°,则点B的坐标为($\sqrt{2}$,$-\sqrt{2}$).
如图,以原点为圆心,2为半径的⊙O与正半轴交于点A,在⊙O上且在x轴的下方有一点B,∠AOB=45°,则点B的坐标为($\sqrt{2}$,$-\sqrt{2}$).
分析 过点B作BC⊥y轴,垂足为C,利用特殊锐角三角函数值可求得OC、CB的长,从而得到点B的坐标.
解答 解:过点B作BC⊥y轴,垂足为C.
∵∠AOB=45°,
∴∠OBC=45°.
∴OC=cos45°•OB=$\frac{\sqrt{2}}{2}$×2=$\sqrt{2}$,BC=sin45°•OB=$\frac{\sqrt{2}}{2}×2$=$\sqrt{2}$.
所以点B的坐标为($\sqrt{2}$,-$\sqrt{2}$).
故答案为:($\sqrt{2}$,-$\sqrt{2}$).
点评 本题主要考查的是特殊锐角三角函数,掌握特殊锐角三角函数值是解题的关键.

练习册系列答案
相关题目
19.把-(x-y)-z去括号得( )
| A. | -x+y-z | B. | -x-y-z | C. | -x+y+z | D. | -x-y+z |
 如图,AB∥CD,AE交DE于点C,DE⊥AE,垂足为E,∠A=41°,求∠D的度数.
如图,AB∥CD,AE交DE于点C,DE⊥AE,垂足为E,∠A=41°,求∠D的度数.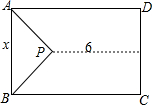 如图,一块矩形空地ABCD,除留下一块等腰直角△APB的空地外,其他都种植草皮.设AB=x米,直角顶点P到CD的距离为6米,草地的面积为y米2,求y与x之间的函数关系式.
如图,一块矩形空地ABCD,除留下一块等腰直角△APB的空地外,其他都种植草皮.设AB=x米,直角顶点P到CD的距离为6米,草地的面积为y米2,求y与x之间的函数关系式.