题目内容
7. 如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数$y=\frac{k}{x}$(x>0)的图象经过点D.已知S△BCE=2,则k的值是( )
如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数$y=\frac{k}{x}$(x>0)的图象经过点D.已知S△BCE=2,则k的值是( )| A. | 2 | B. | -2 | C. | 3 | D. | 4 |
分析 设D点坐标为(m,n),则AB=CD=m,由平行四边形的性质可得出∠BAC=∠CEO,结合∠BCA=∠COE=90°,即可证出△ABC∽△ECO,根据相似三角形的性质可得出BC•EC=AB•CO=mn,再根据S△BCE=2即可求出k=4,此题得解.
解答 解:设D点坐标为(m,n),则AB=CD=m,
∵CD平行于x轴,AB∥CD,
∴∠BAC=∠CEO.
∵BC⊥AC,∠COE=90°,
∴∠BCA=∠COE=90°,
∴△ABC∽△ECO,
∴$\frac{AB}{EC}$=$\frac{BC}{CO}$,
∴BC•EC=AB•CO=mn.
∵点D在反比例函数y=$\frac{k}{x}$的图象上,
∴k=mn=BC•EC=2S△BCE=4.
故选D.
点评 本题考查了反比例函数图象上点的坐标特征、平行四边形的性质以及相似三角形的判定与性质,由△ABC∽△ECO得出k=mn=BC•EC是解题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
15.下列计算正确的是( )
| A. | 4a+5b=9ab | B. | (a3)5=a15 | C. | a4•a2=a8 | D. | a6÷a3=a2 |
2. 如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为( )
 如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角为α度,AC=7米,则树高BC为( )| A. | 7sinα米 | B. | 7cosα米 | C. | 7tanα米 | D. | (7+α)米 |
19.用配方法解一元二次方程2x2-x-l=0时,配方正确的是( )
| A. | (x-$\frac{1}{4}$)2=$\frac{9}{16}$ | B. | (x+$\frac{1}{4}$)2=$\frac{9}{16}$ | C. | (x-$\frac{1}{2}$)2=$\frac{5}{4}$ | D. | (x+$\frac{1}{2}$)2=$\frac{5}{4}$ |
16.下列事件:
①在足球赛中,弱队战胜强队;
②抛掷一枚硬币,落地后正面朝上;
③任取两个整数,其和大于1;
④长分别为2、4、8厘米的三条线段能围成一个三角形.
其中确定事件的个数是( )
①在足球赛中,弱队战胜强队;
②抛掷一枚硬币,落地后正面朝上;
③任取两个整数,其和大于1;
④长分别为2、4、8厘米的三条线段能围成一个三角形.
其中确定事件的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17. 已知圆锥的底面半径为5,母线长为8,则该圆锥的侧面积为( )
已知圆锥的底面半径为5,母线长为8,则该圆锥的侧面积为( )
 已知圆锥的底面半径为5,母线长为8,则该圆锥的侧面积为( )
已知圆锥的底面半径为5,母线长为8,则该圆锥的侧面积为( )| A. | 80π | B. | 40π | C. | 105π | D. | 65π |
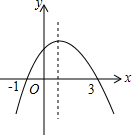 如图所示是二次函数y=ax2+bx+c(a≠0)的图象,现有下列说法:
如图所示是二次函数y=ax2+bx+c(a≠0)的图象,现有下列说法: 如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,EF与AC交于点O,分别连接AE、CF.若AB=$\sqrt{3}$,∠DCF=30°,则EF的长为2.
如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,EF与AC交于点O,分别连接AE、CF.若AB=$\sqrt{3}$,∠DCF=30°,则EF的长为2.