题目内容
12. 如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,EF与AC交于点O,分别连接AE、CF.若AB=$\sqrt{3}$,∠DCF=30°,则EF的长为2.
如图,将矩形纸片ABCD折叠,使点A与点C重合,折痕为EF,EF与AC交于点O,分别连接AE、CF.若AB=$\sqrt{3}$,∠DCF=30°,则EF的长为2.
分析 先根据解直角三角形得到DF和CF的长,再根据勾股定理求得AC的长,并得出AO的长,然后利用勾股定理求得OF的长,最后根据等腰三角形的性质,求得EF的长等于OF长的2倍.
解答  解:∵矩形ABCD中,AB=CD=$\sqrt{3}$,∠D=90°,
解:∵矩形ABCD中,AB=CD=$\sqrt{3}$,∠D=90°,
∴DF=1,CF=2,
由折叠可得,AC被EF垂直平分,
∴AF=CF=2,
∴AD=2+1=3,
∴直角三角形ACD中,AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{3}^{2}+(\sqrt{3})^{2}}$=$2\sqrt{3}$,
∴AO=$\frac{1}{2}$AC=$\sqrt{3}$,
∴直角三角形AOF中,OF=$\sqrt{{2}^{2}-(\sqrt{3})^{2}}$=1,
又∵由折叠得∠AEO=∠CEO,由AD∥BC得∠AFO=∠CEO,
∴∠AFO=∠AEO,即AF=AE,
∵AO⊥EF,
∴EF=2FO=2,
故答案为:2.
点评 本题主要考查了矩形的性质以及折叠的性质:折叠前后两图形全等,即对应线段相等,对应角相等.解题时注意:对应点的连线段被折痕垂直平分.此题也可以通过判定△AEF为等边三角形进行求解.

练习册系列答案
相关题目
3.下列各图不是正方体表面展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
7. 如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数$y=\frac{k}{x}$(x>0)的图象经过点D.已知S△BCE=2,则k的值是( )
如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数$y=\frac{k}{x}$(x>0)的图象经过点D.已知S△BCE=2,则k的值是( )
 如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数$y=\frac{k}{x}$(x>0)的图象经过点D.已知S△BCE=2,则k的值是( )
如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连接BE,反比例函数$y=\frac{k}{x}$(x>0)的图象经过点D.已知S△BCE=2,则k的值是( )| A. | 2 | B. | -2 | C. | 3 | D. | 4 |
4.若代数式$\frac{1}{x+2}$有意义,则x的取值范围是( )
| A. | x≠0 | B. | x≠2 | C. | x≠-2 | D. | x>-2 |
1. 如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )
如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )
 如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )
如图,AB为⊙O的直径,C为⊙O外一点,过点C作⊙O的切线,切点为B,连结AC交⊙O于D,∠C=38°.点E在AB右侧的半圆上运动(不与A、B重合),则∠AED的大小是( )| A. | 62° | B. | 52° | C. | 38° | D. | 28° |
2. 一个长方体的主视图、俯视图如图所示(单位:cm),则其左视图的面积为( )
一个长方体的主视图、俯视图如图所示(单位:cm),则其左视图的面积为( )
 一个长方体的主视图、俯视图如图所示(单位:cm),则其左视图的面积为( )
一个长方体的主视图、俯视图如图所示(单位:cm),则其左视图的面积为( )| A. | 36cm2 | B. | 40cm2 | C. | 90cm2 | D. | 36或40cm2 |
 如图,在⊙O中,点A为$\widehat{BC}$的中点,若∠BAC=140°,则∠OBA的度数为70°.
如图,在⊙O中,点A为$\widehat{BC}$的中点,若∠BAC=140°,则∠OBA的度数为70°. 在平面直角坐标系中,已知点A(-1,0),B(-2,2),请在图中画出线段AB,并画出线段AB绕点O逆时针旋转90°后的图形.
在平面直角坐标系中,已知点A(-1,0),B(-2,2),请在图中画出线段AB,并画出线段AB绕点O逆时针旋转90°后的图形.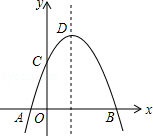 如图,抛物线y=-x2+2x+m+1交x轴与点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题:
如图,抛物线y=-x2+2x+m+1交x轴与点A(a,0)和B(b,0),交y轴于点C,抛物线的顶点为D,下列四个命题: