题目内容
11.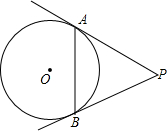 如图,PA、PB是圆O的切线,切点分别是A、B,如果∠P=60°,那么弦AB所对的圆周角等于( )
如图,PA、PB是圆O的切线,切点分别是A、B,如果∠P=60°,那么弦AB所对的圆周角等于( )| A. | 60° | B. | 120° | C. | 30°或120° | D. | 60°或120° |
分析 由PA、PB是⊙O的切线,∠P=60°,根据切线的性质,易求得∠AOB的度数,然后由圆周角定理,可求得当点C在优弧AB上时,∠ACB的值,由圆的内接四边形的性质,可求得当点C在劣弧AB上时,∠ACB的度数,继而求得答案.
解答  解:连接OA、OB,
解:连接OA、OB,
∵PA、PB是⊙O的切线,
∴OA⊥PA,OB⊥PB,
∴∠PAO=∠PBO=90°,
∵∠P=60°,
∴∠AOB=360°-∠PAO-∠PBO-∠P=120°,
∴当点C在优弧AB上时,∠ACB=$\frac{1}{2}$∠AOB=60°;
当点C在劣弧AB上时,∠ACB=180°-60°=120°.
∴弦BA所对的圆周角的度数是:60°或120°.
故选D.
点评 此题考查了切线的性质、圆周角定理以及圆的内接四边形的性质.此题难度不大,注意掌握弦所对的圆周角有两种且互补.

练习册系列答案
相关题目
1.计算12a5b6c4÷(-3a2b3c)÷(2a3b3c3),其结果是( )
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
19. 如图,E是AB上一点,F是DC上一点,G是BC延长线上一点,下列能判断AB∥CD的是( )
如图,E是AB上一点,F是DC上一点,G是BC延长线上一点,下列能判断AB∥CD的是( )
 如图,E是AB上一点,F是DC上一点,G是BC延长线上一点,下列能判断AB∥CD的是( )
如图,E是AB上一点,F是DC上一点,G是BC延长线上一点,下列能判断AB∥CD的是( )| A. | ∠A+∠B=180° | B. | ∠D=∠DCG | C. | ∠B=∠DCG | D. | ∠B=∠AEF |
3.下列是二次函数的是( )
| A. | y=2(x+1)2 | B. | y=4x2-(2x+1)2 | C. | y=$\frac{{x}^{2}}{x}$ | D. | y=$\frac{1}{{x}^{2}}$ |
1.抛物线y=$\frac{1}{2}$x2的图象向左平移2个单位,在向下平移1个单位,得到的函数表达式为( )
| A. | y=$\frac{1}{2}$x2+2x+1 | B. | y=$\frac{1}{2}$x2+2x-2 | C. | y=$\frac{1}{2}$x2-2x-1 | D. | y=$\frac{1}{2}$x2-2x+1 |