题目内容
2.我校高中部开展了丰富多彩的社团活动,刚升高一的李明同学喜欢其中的书法社及篮球社,他不知如何选择,最后他决定通过掷硬币决定,规则如下:连续抛掷硬币三次,如果三次正面向上或反面向上,则两个都去;如果两次正面向上一次反面向上,则选择书法社;如果两次反面向上一次正面向上,则选择篮球社.(1)用画树状图的方法表示三次抛掷硬币的所有结果;
(2)李明两门课都选择的概率有多大;
(3)李明用这个游戏规则去选择去哪个社团是否合理?为什么?
分析 (1)利用树状图可展示所有8种等可能的结果数;
(2)找出三次正面向上或反面向上的结果数,然后根据概率公式求解;
(3)分别计算出选择书法社的概率和选择篮球社的概率,然后比较它们的大小即可判断用这个游戏规则去选择去哪个社团是否合理.
解答 解:(1)画树状图为:
共有8种等可能的结果数;
(2)三次正面向上或反面向上的结果数为2,
所以李明两门课都选择的概率=$\frac{2}{8}$=$\frac{1}{4}$;
(3)因为两次正面向上一次反面向上的结果数为3,则选择书法社的概率=$\frac{3}{8}$;
两次反面向上一次正面向上的结果数为3,则选择篮球社的概率=$\frac{3}{8}$,
所以用这个游戏规则去选择去哪个社团是合理的.
点评 本题考查了列表法与树状图法:利用列表法和树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
17.已知m-n=-1,则(m-n)2+3(n-m)+2的值是( )
| A. | 6 | B. | 4 | C. | 0 | D. | 2 |
7.若-4a5b2m与3a2m+3bn+3的和仍一个是单项式,则m、n的值分别是( )
| A. | 1,-1 | B. | 1,2 | C. | 1,-2 | D. | 1,1 |
14.下列各式没有意义的是( )
| A. | $\sqrt{3^2}$ | B. | $\sqrt{-{3^2}}$ | C. | $\sqrt{{{({-3})}^2}}$ | D. | ${({\sqrt{3}})^2}$ |
11.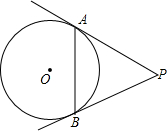 如图,PA、PB是圆O的切线,切点分别是A、B,如果∠P=60°,那么弦AB所对的圆周角等于( )
如图,PA、PB是圆O的切线,切点分别是A、B,如果∠P=60°,那么弦AB所对的圆周角等于( )
 如图,PA、PB是圆O的切线,切点分别是A、B,如果∠P=60°,那么弦AB所对的圆周角等于( )
如图,PA、PB是圆O的切线,切点分别是A、B,如果∠P=60°,那么弦AB所对的圆周角等于( )| A. | 60° | B. | 120° | C. | 30°或120° | D. | 60°或120° |
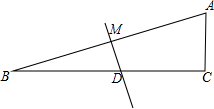 如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于点D,交AB于点M,BD=8cm,求AC的长.
如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于点D,交AB于点M,BD=8cm,求AC的长.