题目内容
已知直线L1:y=
x+5与坐标轴交于A、B两点,直线L2:y=-2x+10与坐标轴交于C、D两点,两直线交于点P.
(1)求P点坐标;
(2)判别△PAC的形状,并说明理由;
(3)在x轴上是否存在点Q,使△PAQ是等腰三角形?若存在,请直接写出Q点的坐标.
| 1 |
| 2 |
(1)求P点坐标;
(2)判别△PAC的形状,并说明理由;
(3)在x轴上是否存在点Q,使△PAQ是等腰三角形?若存在,请直接写出Q点的坐标.
考点:一次函数综合题
专题:
分析:(1)将y=
x+5和y=-2x+10组成方程组,方程组的解就是交点坐标;
(2)根据系数的积的比为-1,判断出两直线垂直,得到△PAC为直角三角形.
(3)过P作PE⊥x轴于E,E点坐标为(2,0),根据勾股定理求出PA的长,直接求出Q1,Q2,Q4,作GQ3⊥AP,求出GQ3解析式,得到Q3的坐标.
| 1 |
| 2 |
(2)根据系数的积的比为-1,判断出两直线垂直,得到△PAC为直角三角形.
(3)过P作PE⊥x轴于E,E点坐标为(2,0),根据勾股定理求出PA的长,直接求出Q1,Q2,Q4,作GQ3⊥AP,求出GQ3解析式,得到Q3的坐标.
解答: 解:如图:
解:如图:
(1)将y=
x+5和y=-2x+10组成方程组得
,
解得
,
可得P(2,6).
(2)∵L1:y=
x+5的比例系数为k,L2:y=-2x+10的比例系数为-2,
可得
×(-2)=-1,
∴∠APC=90°,△PAC为直角三角形.
(3)过P作PE⊥x轴于E,
E点坐标为(2,0).
∵P(2,6),A(-10,0),
∴PA=
=6
,
∴可见,OQ1=6
-10,
Q1(6
-10,0),Q2(-6
-10,0),
作GQ3⊥AP,设GQ3解析式为y=-2x+b,H坐标为(-4,3),
将H(-4,3)代入y=-2x+b得,3=-2×(-4)+b,
解得b=-5,
∴y=-2x-5,
当y=0时,x=-
,Q3(-
,0),Q4(2+6
,0).
 解:如图:
解:如图:(1)将y=
| 1 |
| 2 |
|
解得
|
可得P(2,6).
(2)∵L1:y=
| 1 |
| 2 |
可得
| 1 |
| 2 |
∴∠APC=90°,△PAC为直角三角形.
(3)过P作PE⊥x轴于E,
E点坐标为(2,0).
∵P(2,6),A(-10,0),
∴PA=
| 62+122 |
| 5 |
∴可见,OQ1=6
| 5 |
Q1(6
| 5 |
| 5 |
作GQ3⊥AP,设GQ3解析式为y=-2x+b,H坐标为(-4,3),
将H(-4,3)代入y=-2x+b得,3=-2×(-4)+b,
解得b=-5,
∴y=-2x-5,
当y=0时,x=-
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
点评:本题考查了一次函数综合题,熟悉函数和方程的关系,充分利用图形,根据一次函数的特点,分别求出各点的坐标再计算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

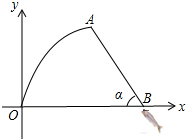 某市举行钓鱼比赛,如图,选手甲钓到了一条大鱼,鱼竿被拉弯近似可看作以A为最高点的一条抛物线,鱼线AB长6m,鱼隐约在水面了,估计鱼离鱼竿支点有8m,此时鱼竿鱼线呈一个平面,且与水平面夹脚α恰好为60°,以鱼竿支点为原点,求鱼竿所在抛物线的解析式.
某市举行钓鱼比赛,如图,选手甲钓到了一条大鱼,鱼竿被拉弯近似可看作以A为最高点的一条抛物线,鱼线AB长6m,鱼隐约在水面了,估计鱼离鱼竿支点有8m,此时鱼竿鱼线呈一个平面,且与水平面夹脚α恰好为60°,以鱼竿支点为原点,求鱼竿所在抛物线的解析式.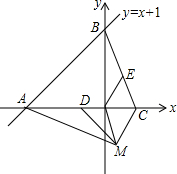 如图,在平面直角坐标系中直线y=x+1与坐标轴交于AB两点,AB=AC,D、E分别为AC、BC的中点,作∠CDM=45°,AM⊥CM,
如图,在平面直角坐标系中直线y=x+1与坐标轴交于AB两点,AB=AC,D、E分别为AC、BC的中点,作∠CDM=45°,AM⊥CM,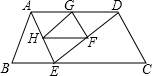 如图,在等腰梯形ABCD中,AD∥BC,∠B=60°,AB=2,AD=3,点E是线段BC上的一个动点(E与B、C不重合),G、F、H分别是AD、DE、AE的中点,连接HG、GF、FH.
如图,在等腰梯形ABCD中,AD∥BC,∠B=60°,AB=2,AD=3,点E是线段BC上的一个动点(E与B、C不重合),G、F、H分别是AD、DE、AE的中点,连接HG、GF、FH.