题目内容
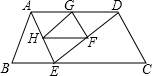 如图,在等腰梯形ABCD中,AD∥BC,∠B=60°,AB=2,AD=3,点E是线段BC上的一个动点(E与B、C不重合),G、F、H分别是AD、DE、AE的中点,连接HG、GF、FH.
如图,在等腰梯形ABCD中,AD∥BC,∠B=60°,AB=2,AD=3,点E是线段BC上的一个动点(E与B、C不重合),G、F、H分别是AD、DE、AE的中点,连接HG、GF、FH.(1)求证:△GHF≌△EFH;
(2)①当BE=
②∠AED的度数为
考点:等腰梯形的性质,全等三角形的判定与性质,三角形中位线定理,菱形的判定,矩形的判定
专题:
分析:(1)根据三角形中位线的性质可得GF=HE,HG=EF,再利用SSS定理证明△GHF≌△EFH;
(2)①过A作AM⊥BC,过D作DN⊥BC,可构造矩形AMND,进而得到MN=AD=3,再求出BC长,可判定△ABE≌△DCE得到AE=DE,再证明四边形GHEF是平行四边形,然后证明GH=GF可得四边形GHEF是菱形;②根据有一个角是直角的平行四边形是矩形可得∠AED=90°.
(2)①过A作AM⊥BC,过D作DN⊥BC,可构造矩形AMND,进而得到MN=AD=3,再求出BC长,可判定△ABE≌△DCE得到AE=DE,再证明四边形GHEF是平行四边形,然后证明GH=GF可得四边形GHEF是菱形;②根据有一个角是直角的平行四边形是矩形可得∠AED=90°.
解答:(1)证明:∵G、F、H分别是AD、DE、AE的中点,
∴GF=
AE,HE=
AE,HG=
ED,EF=
DE,
∴GF=HE,HG=EF,
在△GHF和△EFH中,
∴△GHF≌△EFH(SSS);
(2)解:①当BE=2.5时,四边形GHEF是菱形;
过A作AM⊥BC,过D作DN⊥BC,
∴∠AMN=∠DNB=90°,
∵AD∥BC,
∴∠DAM=90°,
∴四边形AMND是矩形,
∴MN=3,
∵∠B=60°,
∴∠BAM=30°,
∵AB=2,
∴BM=1,
同理CN=1,
∴BC=5,
∵EB=2.5,
∴EC=2.5,
在△ABE和△DCE中,
,
∴△ABE≌△DCE(SAS),
∴AE=DE,
∵G、F、H分别是AD、DE、AE的中点,
∴GH∥DE,GH=
DE,FG∥AE,FG=
AE,
∴四边形GHEF是平行四边形,
∵AE=ED,
∴GH=GF,
∴四边形GHEF是菱形;
②∠AED的度数为90°时,四边形GHFD为矩形,
∵四边形GHEF是平行四边形,
∠AED=90°,
∴四边形GHFD为矩形.
∴GF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴GF=HE,HG=EF,
在△GHF和△EFH中,
|
∴△GHF≌△EFH(SSS);
(2)解:①当BE=2.5时,四边形GHEF是菱形;
过A作AM⊥BC,过D作DN⊥BC,
∴∠AMN=∠DNB=90°,
∵AD∥BC,
∴∠DAM=90°,
∴四边形AMND是矩形,
∴MN=3,
∵∠B=60°,
∴∠BAM=30°,
∵AB=2,
∴BM=1,
同理CN=1,
∴BC=5,
∵EB=2.5,
∴EC=2.5,
在△ABE和△DCE中,
|

∴△ABE≌△DCE(SAS),
∴AE=DE,
∵G、F、H分别是AD、DE、AE的中点,
∴GH∥DE,GH=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形GHEF是平行四边形,
∵AE=ED,
∴GH=GF,
∴四边形GHEF是菱形;
②∠AED的度数为90°时,四边形GHFD为矩形,
∵四边形GHEF是平行四边形,
∠AED=90°,
∴四边形GHFD为矩形.
点评:此题主要考查了等腰梯形的性质,以及菱形和矩形的判定,关键是作出辅助线,构造矩形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
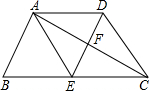 如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED,AC与ED相交于点F.求证:梯形ABCD是等腰梯形.
如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED,AC与ED相交于点F.求证:梯形ABCD是等腰梯形.
