题目内容
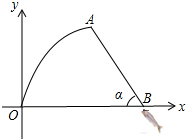 某市举行钓鱼比赛,如图,选手甲钓到了一条大鱼,鱼竿被拉弯近似可看作以A为最高点的一条抛物线,鱼线AB长6m,鱼隐约在水面了,估计鱼离鱼竿支点有8m,此时鱼竿鱼线呈一个平面,且与水平面夹脚α恰好为60°,以鱼竿支点为原点,求鱼竿所在抛物线的解析式.
某市举行钓鱼比赛,如图,选手甲钓到了一条大鱼,鱼竿被拉弯近似可看作以A为最高点的一条抛物线,鱼线AB长6m,鱼隐约在水面了,估计鱼离鱼竿支点有8m,此时鱼竿鱼线呈一个平面,且与水平面夹脚α恰好为60°,以鱼竿支点为原点,求鱼竿所在抛物线的解析式.考点:二次函数的应用
专题:
分析:过点A作AC⊥OB,交OB于点C,在Rt△ABC中,可求出AC、BC,然后根据OB=8米,可得出点A的坐标,根据二次函数过原点及二次函数的顶点坐标即可确定二次函数解析式.
解答: 解:过点A作AC⊥OB,交OB于点C,
解:过点A作AC⊥OB,交OB于点C,
∵AB=6米,OB=8米,α=60°,
∴AC=ABsin∠α=3
米,BC=ACcos∠α=3米,
∴OC=OB-BC=5米,
故可得点A的坐标为(5,3
),
设函数解析式为y=a(x-5)2+3
,
又∵函数经过原点,
∴a(0-5)2+3
=0,
解得:a=-
.
故函数解析式为:y=-
(x-5)2+3
.
 解:过点A作AC⊥OB,交OB于点C,
解:过点A作AC⊥OB,交OB于点C,∵AB=6米,OB=8米,α=60°,
∴AC=ABsin∠α=3
| 3 |
∴OC=OB-BC=5米,
故可得点A的坐标为(5,3
| 3 |
设函数解析式为y=a(x-5)2+3
| 3 |
又∵函数经过原点,
∴a(0-5)2+3
| 3 |
解得:a=-
3
| ||
| 25 |
故函数解析式为:y=-
3
| ||
| 25 |
| 3 |
点评:此题考查了二次函数的应用,关键是利用几何知识求出点A的坐标,另外要掌握二次函数的一般式及顶点式的特点,有一定难度.

练习册系列答案
相关题目
 把14个棱长为1的正方体,在地面上堆叠成如图所示的立方体,然后将露出的表面部分染成红色,那么红色部分的面积为( )
把14个棱长为1的正方体,在地面上堆叠成如图所示的立方体,然后将露出的表面部分染成红色,那么红色部分的面积为( )| A、21 | B、24 | C、33 | D、37 |
 如图,在等腰Rt△ABC中,∠A=90°,AC=7,点O在AC上,且AO=2,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转90°,得到线段OD,要使点D恰好落在BC上,则AP的长等于
如图,在等腰Rt△ABC中,∠A=90°,AC=7,点O在AC上,且AO=2,点P是AB上一动点,连接OP,将线段OP绕点O逆时针旋转90°,得到线段OD,要使点D恰好落在BC上,则AP的长等于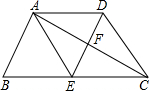 如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED,AC与ED相交于点F.求证:梯形ABCD是等腰梯形.
如图,在梯形ABCD中,AD∥BC,E为BC的中点,BC=2AD,EA=ED,AC与ED相交于点F.求证:梯形ABCD是等腰梯形.