题目内容
12.已知抛物线y=-x2+3x+c与x轴相交于A(m,0)、B(n,0)两点,则m+n=3.分析 先根据抛物线上两点的纵坐标相等可知此两点关于对称轴对称,再根据中点坐标公式求出这两点横坐标的中点坐标就是对称轴.
解答 解:∵抛物线y=-x2+3x+c的对称轴x=$\frac{3}{2}$,点A(m,0),B(n,0)是抛物线y=-x2+3x+c上的两点,
∴$\frac{m+n}{2}$=$\frac{3}{2}$,
∴m+n=3.
故答案为:3.
点评 本题考查二次函数图象上点的坐标特征,二次函数的性质,根据题意判断出抛物线上对称两点坐标的关系是解答此题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
7.在△ABC中,∠A=62°,点I是外接圆圆心,则∠BIC=124度.
在△ABC中,O是△ABC的内心,若∠A=50°,则∠BOC=115°.
一个三角形的外心与内心恰好重合,这个三角形是等边三角形.
在△ABC中,O是△ABC的内心,若∠A=50°,则∠BOC=115°.
一个三角形的外心与内心恰好重合,这个三角形是等边三角形.
17.已知二次函数y=ax2+bx+c的y与x的部分对应值如下表:则下列判断中正确的是( )
| x | … | -2 | 0 | 1 | 2 | … |
| y | … | 7 | -1 | -2 | -1 | … |
| A. | 抛物线开口向下 | B. | 抛物线的对称轴是y轴 | ||
| C. | x<1时,y随x的增大而减小 | D. | 抛物线与y轴交于正半轴 |
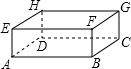 如图,长方体的长、宽、高分别为6cm,5cm,4cm,现有一只蜘蛛由A出发去捕食G处的昆虫,则这只蜘蛛的最短爬行路线的长为3$\sqrt{13}$cm.
如图,长方体的长、宽、高分别为6cm,5cm,4cm,现有一只蜘蛛由A出发去捕食G处的昆虫,则这只蜘蛛的最短爬行路线的长为3$\sqrt{13}$cm. 如图,在⊙O中,AB=AC,∠B=70°,则∠C=70°.
如图,在⊙O中,AB=AC,∠B=70°,则∠C=70°.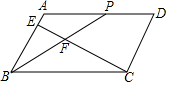 已知,如图?ABCD中,AB=5,BP平分∠ABC,CE⊥AB,垂足为E点,交BP于F点,若tan∠PFC=$\frac{4}{3}$,则BP=8.
已知,如图?ABCD中,AB=5,BP平分∠ABC,CE⊥AB,垂足为E点,交BP于F点,若tan∠PFC=$\frac{4}{3}$,则BP=8.