题目内容
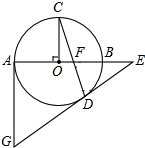 如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.
如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.(1)求证:∠C+∠EDF=90°
(2)已知:AG=6,⊙O的半径为3,求OF的值.
考点:切线的性质
专题:
分析:(1)连接OD,根据切线的性质得OD⊥DE,则∠EDF+∠ODC=90°,而∠C=∠ODC,则∠EDF+∠C=90°.
(2)先求得EF=ED,设DE=x,则EF=x,根据切线的性质由AG为⊙O的切线得∠ODE=90°,再证明Rt△EOD∽Rt△EGA,利用相似比求得AE=2x,OE=3+
x,然后根据AE-OE=OA=3,求得x的值,进而求得OF=1.
(2)先求得EF=ED,设DE=x,则EF=x,根据切线的性质由AG为⊙O的切线得∠ODE=90°,再证明Rt△EOD∽Rt△EGA,利用相似比求得AE=2x,OE=3+
| 1 |
| 2 |
解答: (1)证明:连接OD,
(1)证明:连接OD,
∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,即∠EDF+∠ODC=90°,
∵OC=OD,
∴∠C=∠ODC,
∴∠C+∠EDF=90°.
(2)解:∵∠C+∠EDF=90°,∠C+∠CFO=90°,∠CFO=∠EFD,
∴∠EFD=∠EDF,
∴EF=ED,
设DE=x,则EF=x,
∵∠ODE=∠GAE,∠OED=∠GEA,
∴Rt△EOD∽Rt△EGA,
∴
=
=
,即
=
=
,
∴AE=2x,OE=3+
x,
∵AE-OE=OA=3,
∴2x-(3+
x)=3,解得x=4,
∴AE=2x=8,
∴OF=AE-EF-OA=8-3-4=1.
 (1)证明:连接OD,
(1)证明:连接OD,∵DE为⊙O的切线,
∴OD⊥DE,
∴∠ODE=90°,即∠EDF+∠ODC=90°,
∵OC=OD,
∴∠C=∠ODC,
∴∠C+∠EDF=90°.
(2)解:∵∠C+∠EDF=90°,∠C+∠CFO=90°,∠CFO=∠EFD,
∴∠EFD=∠EDF,
∴EF=ED,
设DE=x,则EF=x,
∵∠ODE=∠GAE,∠OED=∠GEA,
∴Rt△EOD∽Rt△EGA,
∴
| OD |
| AG |
| DE |
| AE |
| OE |
| GE |
| 3 |
| 6 |
| x |
| AE |
| OE |
| 6+x |
∴AE=2x,OE=3+
| 1 |
| 2 |
∵AE-OE=OA=3,
∴2x-(3+
| 1 |
| 2 |
∴AE=2x=8,
∴OF=AE-EF-OA=8-3-4=1.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了相似三角形的判定与性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,两个正方形的边长分别为4,3,两阴影部分的面积分别为a,b(a>b),则a-b等于( )
如图,两个正方形的边长分别为4,3,两阴影部分的面积分别为a,b(a>b),则a-b等于( )| A、7 | B、6 | C、5 | D、4 |
 如图,⊙A,⊙B,⊙C两两不相交,且半径都是1cm,则图中的三个扇形(即阴影部分)的面积之和为( )
如图,⊙A,⊙B,⊙C两两不相交,且半径都是1cm,则图中的三个扇形(即阴影部分)的面积之和为( )A、
| ||
B、
| ||
| C、π | ||
| D、π |
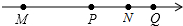 如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )
如图,四个有理数在数轴上的对应点M,P,N,Q,若点M,N表示的有理数互为相反数,则图中表示绝对值最小的数的点是( )| A、点M | B、点N | C、点P | D、点Q |
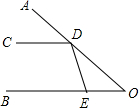 如图所示,∠AOB的两边OA,OB均为平面反光镜,∠AOB=30°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行.
如图所示,∠AOB的两边OA,OB均为平面反光镜,∠AOB=30°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行.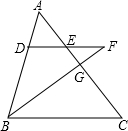 已知如图,D是△ABC的边AB上一点,DE∥BC,交边AC于点E,延长DE至点F,使EF=DE,联结BF,交边AC于点G,联结CF
已知如图,D是△ABC的边AB上一点,DE∥BC,交边AC于点E,延长DE至点F,使EF=DE,联结BF,交边AC于点G,联结CF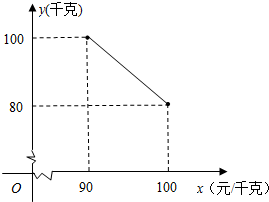 某茶叶专卖店经销一种崂山绿茶,每千克成本80元.据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.
某茶叶专卖店经销一种崂山绿茶,每千克成本80元.据销售人员调查发现,每月的销售量y(千克)与销售单价x(元/千克)之间存在如图所示的变化规律.