题目内容
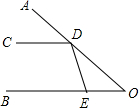 如图所示,∠AOB的两边OA,OB均为平面反光镜,∠AOB=30°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行.
如图所示,∠AOB的两边OA,OB均为平面反光镜,∠AOB=30°,在OB上有一点E,从E点射出一束光线经OA上的点D反射后,反射光线DC恰好与OB平行.(1)求∠DEB的度数;
(2)若从E点的光线垂直OB射出,经OA上的点F反射后,反射光线与OB相交于点M,求∠EFM的度数.
考点:平行线的性质
专题:
分析:(1)如图1,作出法线,运用平面镜的反射原理,证明∠1=∠3,进而得到∠2=∠3,借助三角形的内角和定理即可解决问题.
(2)如图2,求出∠EFO=60°,借助反射原理即可解决问题.
(2)如图2,求出∠EFO=60°,借助反射原理即可解决问题.
解答:
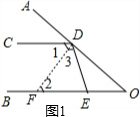 解:(1)如图1,过点D作DF⊥AO交OB于点F.
解:(1)如图1,过点D作DF⊥AO交OB于点F.
∵入射角等于反射角,
∴∠1=∠3,
∵CD∥OB,
∴∠1=∠2(两直线平行,内错角相等);
∴∠2=∠3(等量代换);
在Rt△DOF中,∠ODF=90°,∠AOB=30°,
∴∠2=60°;
∴在△DEF中,∠DEB=180°-2∠2=60°.
(2)如图2,∵EF⊥OB,且∠O=30°,
∴∠EFO=90°-30°=60°;
∴∠EFM=2(90°-60°)=60°.

 解:(1)如图1,过点D作DF⊥AO交OB于点F.
解:(1)如图1,过点D作DF⊥AO交OB于点F.∵入射角等于反射角,
∴∠1=∠3,
∵CD∥OB,
∴∠1=∠2(两直线平行,内错角相等);
∴∠2=∠3(等量代换);
在Rt△DOF中,∠ODF=90°,∠AOB=30°,
∴∠2=60°;
∴在△DEF中,∠DEB=180°-2∠2=60°.
(2)如图2,∵EF⊥OB,且∠O=30°,
∴∠EFO=90°-30°=60°;
∴∠EFM=2(90°-60°)=60°.
点评:本题考查了平行线的性质的应用,解此题的关键是能找到法线,再根据法线的性质解决问题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
下列运算中,错误的是( )
| A、a2÷a-3=a5 | ||||
| B、(-2a2)3=-8x6 | ||||
C、(
| ||||
| D、2x2-x2=1 |
 如图,△ABC为等边三角形,BD⊥AC于点D,点E在BC的延长线上,CE=CD,△ABC的周长为6,BD=
如图,△ABC为等边三角形,BD⊥AC于点D,点E在BC的延长线上,CE=CD,△ABC的周长为6,BD=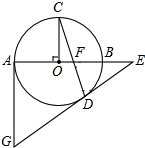 如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.
如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.