题目内容
在△ABC中,AB=AC,点D在BC边上,连接AD,若AD=BD,且△ADC为等腰三角形,则∠BAC的度数为 .
考点:等腰三角形的性质
专题:
分析:由AD=BD得∠BAD=∠DBA,由AB=AC=CD得∠CAD=∠CDA=2∠DBA,∠DBA=∠C,从而可推出∠BAC=3∠DBA,根据三角形的内角和定理即可求得∠DBA的度数,从而不难求得∠BAC的度数.
解答:解:∵AD=BD ,
,
∴设∠BAD=∠B=x°,
∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠B+∠BAD=2∠B,
∴∠ADC≠∠C,
∵△ADC为等腰三角形,
∴AC=DC,
∴∠CAD=∠CDA=2x°,
∴∠BAC=3x°,
∵∠B+∠BAC+∠C=180°
∴5x=180°,
∴x=36°,
∴∠B=36°
∴∠BAC=3∠B=108°.
故答案为108°.
 ,
,∴设∠BAD=∠B=x°,
∵AB=AC,
∴∠B=∠C,
∵∠ADC=∠B+∠BAD=2∠B,
∴∠ADC≠∠C,
∵△ADC为等腰三角形,
∴AC=DC,
∴∠CAD=∠CDA=2x°,
∴∠BAC=3x°,
∵∠B+∠BAC+∠C=180°
∴5x=180°,
∴x=36°,
∴∠B=36°
∴∠BAC=3∠B=108°.
故答案为108°.
点评:此题主要考查学生对等腰三角形的性质及三角形内角和定理的综合运用能力;求得角之间的关系利用内角和求解是正确解答本题的关键.

练习册系列答案
相关题目
 如图,梯形ABCD中,AD∥BC,AB=CD=AD=2,∠B=60°,直线MN为梯形ABCD的对称轴,P为MN上一动点,那么PC+PD的最小值为
如图,梯形ABCD中,AD∥BC,AB=CD=AD=2,∠B=60°,直线MN为梯形ABCD的对称轴,P为MN上一动点,那么PC+PD的最小值为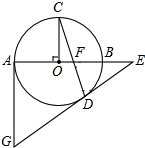 如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.
如图,AB是⊙O直径,OC⊥AB,弦CD与OB交于点F,过点D、A分别作⊙O的切线交于点G,切线GD与AB延长线交于点E.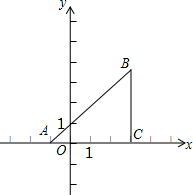 如图,已知直角坐标平面上的△ABC,AC=CB,∠ACB=90°,且A(-1,0),B(m,n),C(3,0).若抛物线y=ax2+bx-3经过A、C两点.
如图,已知直角坐标平面上的△ABC,AC=CB,∠ACB=90°,且A(-1,0),B(m,n),C(3,0).若抛物线y=ax2+bx-3经过A、C两点.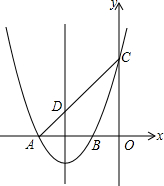 如图,已知抛物线y=x2+6x+5交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(-1,0).
如图,已知抛物线y=x2+6x+5交x轴于A、B两点,交y轴于点C,抛物线的对称轴交x轴于点E,点B的坐标为(-1,0).